Messung von Kernmomenten: Unterschied zwischen den Versionen
| (12 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
<noinclude>{{ScriptProf|Kapitel=6|Abschnitt=0|Prof=Prof. Dr. P. Zimmermann|Thema=Kern- und Strahlungsphysik|Schreiber=Moritz Schubotz}}</noinclude> | <noinclude>{{ScriptProf|Kapitel=6|Abschnitt=0|Prof=Prof. Dr. P. Zimmermann|Thema=Kern- und Strahlungsphysik|Schreiber=Moritz Schubotz}}</noinclude> | ||
Die Messung von Kernmomenten geschieht durch die Messung von | Die Messung von Kernmomenten geschieht durch die Messung von Energieaufspaltungen, die durch die Wechselwirkung der Kernmomente mit | ||
äußeren oder inneratomaren elektromagnetischen Feldern verursacht werden. | äußeren oder inneratomaren elektromagnetischen Feldern verursacht werden. | ||
== äußere Felder: Kernspinresonanzmethode== | ==äußere Felder: Kernspinresonanzmethode== | ||
[[Datei:KernSpinResonanzMethode22.png|miniatur]] | [[Datei:KernSpinResonanzMethode22.png|miniatur|Prinzip der Kernspinresonanzmethode]] | ||
Larmorpräzession <math>\hbar \omega_0 = (\mu_I B_0)</math> | {{FB|Larmorpräzession}} <math>\hbar \omega_0 = (\vec \mu_I \vec B_0)</math> | ||
Größenordnung <math>\nu_0 = \omega_0 / 2 \pi = \mu_K B/h = 7.6 MHz B[T]</math> | |||
Größenordnung | |||
:<math>\begin{align}\nu_0 = \omega_0 / 2 \pi & = \mu_K B/h \\ | |||
& = 7.6 \rm MHz \cdot B[T]\end{align}</math> | |||
Zusätzliches zirkulares Wechselfeld <math>B_1 e^{i \omega t} \bot B_0</math> induziert Übergänge für <math>\omega\approx \omega_0</math> | Zusätzliches zirkulares Wechselfeld <math>B_1 e^{i \omega t} \bot B_0</math> induziert Übergänge für <math>\omega\approx \omega_0</math> | ||
{{AnMS| | |||
;Kernspin: <math>\vec I = \sum \vec l_i + \vec s_i</math> | |||
;Externes homogenes Magnetfeld: <math>\vec B_0 \parallel z </math> | |||
;{{FB|Lamorfrequenz}}: <math>\omega_0</math> | |||
;Kernmoment: <math>\mu_I</math> | |||
;{{FB|Kernmagneton}}: <math>\mu_K</math>}} | |||
'''induzierte Absorption und Emission:''' | |||
Netto-Energieübertrag nur bei unterschiedlicher Besetzung der {{FB|Zeemanniveau}}s durch {{FB|Boltzmann-Verteilung}} im Festkörper. | |||
Boltzmann-Faktor <math>N_1/N_2 = exp(-\Delta E/kT) \approx 1 -\Delta E/kT</math> für <math>\Delta E/kT\le1</math> | |||
Größenordnung z.B. <math>\mu_I\approx \mu_K , B_0 = 1 T, T = 300 K</math> | Größenordnung z.B. <math>\mu_I\approx \mu_K , B_0 = 1 T, T = 300 K</math> | ||
:<math>\Delta E / kT =\mu_K B_0 / kT = \frac{5 10^{-27} J}{1,3 10^{-23} 300 J} \approx 10^ {-6}</math> | :<math>\begin{align} \Delta E / kT =\mu_K B_0 / kT &= \frac{5\cdot 10^{-27} J}{1,3\cdot 10^{-23} \cdot 300 J} \\ | ||
\approx 10^ {-6}\end{align}</math> | |||
{{AnMS|Ist im Umkehrschluss auch eine Temperaturmessung durch Kernspinausrichtung möglich?}} | |||
[[Datei:Zeemannniveaus23.png|miniatur|Induzierte Absorption und Emission]] | |||
---- | |||
===Messung des Kernspins=== | |||
Einschub: Gehört nicht zum Skript (möglicherweise Fehlerbehaftet) | |||
Aus Skript von A.Voßkühler | |||
[[Datei:NMR-Spektrometer.png|miniatur|hochkant=2|Prinzip eines NMR-Spektrometers]] | |||
Die Probe, die aus vielen Atomen bzw. Molekülen bestehen kann, wird in ein externes | |||
homogenes Magnetfeld gegeben. Für die Untersuchung eignen sich alle Atomkerne, die ein | |||
Kernspin aufweisen. | |||
Liegt ein externes Magnetfeld an (in z-Richtung), richten sich die Kernspins nach diesem | |||
Magnetfeld aus, da sie dann die geringste potentielle Energie besitzen. Durch die thermische | |||
Energie der Atome sind die Kernspins nach der Maxwell- Boltzmann- Verteilung ausgerichtet, | |||
mit einer Vorzugsrichtung parallel zum Magnetfeld. Damit ergibt sich eine durchschnittliche | |||
Magnetisierung, die aufgrund der Maxwell- Boltzmann- Verteilung bei Raumtemperatur sehr | |||
klein ist. | |||
In der x/y-Ebene sind eine oder mehrere Spulen angeordnet, mit denen auf die Probe | |||
elektromagnetische Wechselfelder eingestrahlt werden (Sendespule) oder mit denen solche | |||
Felder empfangen werden (Empfangsspule). Durch die Sendespule wird ein starkes, zeitlich | |||
kurzes Magnetfeld aufgebaut, welches senkrecht zum externen Magnetfeld liegt. Die Spins | |||
richten sich an dem neuen Magnetfeld aus und kippen mit der Relaxationszeit in die x/y- | |||
Ebene. Die Dauer des Pulses bestimmt den Winkel, um den die Kernspins gekippt werden. | |||
Wird die Sendespule ausgeschaltet, liegt wieder das normale Magnetfeld vor. In diesem | |||
Magnetfeld präzedieren die Spins mit der Larmorfrequenz, bis sich diese nach einer | |||
Relaxationszeit wieder nach dem Magnetfeld ausrichten. | |||
Die präzedierenden Spins induzieren in der Empfangsspule eine Wechselspannung mit der | |||
Larmorfrequenz, die dann analysiert wird. | |||
====CW-Verfahren==== | |||
Hier wird die eingestrahlte Radiofrequenz langsam durchgestimmt und die Absorption der | |||
Strahlung gemessen. Man arbeitet in der Frequenzdomäne und erhält zunächst ein | |||
Absorptionsspektrum als Funktion der Frequenz. Die Probe wird mit einem extrem schmalen | |||
Signal angeregt. | |||
====Puls-Verfahren==== | |||
Hierbei wird ein einzelner Radiofrequenzimpuls auf die Probe gesandt, die sich in der Spule | |||
befindet. Da der kurze Puls relativ breitbandig ist, werden mit einem Puls viele einzelne | |||
Resonanzen angeregt. Das Signal nach einem Puls oder das Spin-Echo nach zwei oder | |||
mehreren Impulsen, wird als Funktion der Zeit registriert. Mittels Fourier- Transformation wird das | |||
Zeitsignal in ein Spektrum umgewandelt. | |||
====Messung==== | |||
Die Larmorfrequenz des Atoms ist stark von dem lokalen Magnetfeld abhängig. Da alle | |||
Atome unterschiedliche Magnetfelder besitzen, ist die Larmorfrequenz des untersuchten | |||
Atoms stark von der chemischen Umgebung und von der | |||
Bindung abhängig. Durch die Bestimmung der daraus | |||
resultierenden | |||
chemischen | |||
Verschiebung | |||
lassen | |||
sich | |||
Rückschlüsse auf die Bindungspartner und Arten der Bindungen | |||
ziehen. | |||
Die Stärke und die Verteilung mehrerer Resonanzen erlaubt | |||
Rückschlüsse auf die Dichte des Atomes mit einer bestimmten | |||
chemischen Verschiebung in der Probe. | |||
Die Aufspaltungen der Peaks lassen Rückschlüsse über | |||
Wechselwirkungen mit benachbarten Atomgruppen zu. | |||
(Singulett s: keine Aufspaltung, 1 Peak , Duplett d: Aufspaltung in | |||
2 Peaks usw.) | |||
Probleme | |||
Durch die Boltzmannverteilung tragen nur wenige Spins zur | |||
Magnetisierung und damit zum messbaren Signal bei. | |||
Deswegen sind konventionelle NMR-Messungen nur für | |||
Flüssigkeiten oder Festkörper ausgelegt. Für vernünftige | |||
Messungen an einer Atomsorte ist mindestens 1 mol notwendig. | |||
====Noch einmal anders==== | |||
Unter äußerem Magnetfeld spalten die Kernspins | |||
boltzmannverteilt auf. Die meisten Kernspins sitzen unten | |||
parallel zu B. Durch eine Energie in Form von Sendemagnetfeld | |||
mit Larmorfrequenz entsprechend dem ∆E = ϖL können Spins | |||
umgeklappt werden, was das magnetische Moment des | |||
Stoffes ändert und damit eine Spannung induziert. Möchte man | |||
stärkere Effekte haben, muss man die Besetzungsdifferenz | |||
erhöhen, d.h. noch tiefere Temperaturen oder größere | |||
Magnetfelder. Außerdem hilft eine möglichst große Anzahl von Atomen oder Molekülen. | |||
Ende Einschub | |||
== inneratomare Felder der Hüllenelektronen | == inneratomare Felder der Hüllenelektronen == | ||
Hyperfeinstrukturaufspaltung durch Kopplung von Hüllendrehimpuls J und Kernspin I | {{FB|Hyperfeinstrukturaufspaltung}} durch Kopplung von | ||
zu einem Gesamtdrehimpuls F = I + J | *{{FB|Hüllendrehimpuls}} <math>\vec J</math> und | ||
*{{FB|Kernspin}} <math>\vec I</math> zu einem | |||
*{{FB|Gesamtdrehimpuls}} <math>\vec F = \vec I + \vec J</math> | |||
;1. magnetische HFS: | ;1. magnetische HFS: | ||
:<math>\mathcal H = \mu_I B =\frac{\mu_I B}{I J} {I J} = A \ | :<math>\mathcal H = \vec \mu_I \vec B =\frac{\mu_I B}{I J} {\vec I \vec J} = A \tfrac{1}{2}(\vec F^2+\vec I^2+\vec J^2)</math> | ||
:<math>E_F=A \tfrac{1}{2}[F(F + 1) - 1(1 + 1) - J(J + 1)]</math> | :<math>E_F=A \tfrac{1}{2}[F(F + 1) - 1(1 + 1) - J(J + 1)]</math> | ||
{{AnMS|E steht für Energie (Schrödingergleichung und nicht für das elektrische Feld}} | |||
Größenordnung inneratomarer B-Felder der Valenzelektronen etwa | |||
:<math>B=1 - 100 T</math> , z.B. <math>H 1s(17 T), K 4s(63 T), Cs6s(2l0 T)</math>, damit HFS-Aufspaltung | |||
:im Bereich von MHz - GHz. | |||
;2. elektrische, HFS:Wechselwirkung des elektrischen {{FB|Kernquadrupolmoments}} <math>eQ</math> mit dem | |||
:{{FB|elektrischen Feldgradienten}} <math>\varphi = \frac{1}{4 \pi \epsilon_0} \frac{e}{r^3}</math> der Hüllenelektronen (WW von Tensoren 2. Stufe) | |||
Größenordnung | Größenordnung <math>E \approx \frac{1}{4 \pi \epsilon_0} \frac{e}{r^3}</math> mit <math>r^{-3}\approx a_0^{-3}, Q \approx R^2</math> | ||
: <math>E \approx \frac{1}{4 \pi \epsilon_0} \frac{e^2}{a_0 } \left( \frac{R}{a_0}\right)^2\approx27,2 eV 10^{-8}</math> | |||
Da <math>1 eV \leftrightarrow 2,4 \cdot 10^{14} \text{Hz}</math> | |||
:<math>\to E \simeq \rm MHz - GHz</math> | |||
---- | |||
Messung der HFS-Aufspaltung durch '''optische Methoden''' (z.B. {{FB|dopplerfreie Laserspektroskopie}}, Doppelresonanz, Level-Crossing, {{FB|Rabiatomstrahlresonanzmethode}}, {{FB|Mößbauereffekt}}, etc.) | |||
==Weitere Informationen== | |||
(gehört nicht zum Skript) | |||
===Rabi-Experiment=== | |||
*Aufbau:Zwei inhomogene magnetfelder mit gleicher feldaurichtung aber entgegengesetztem feldgradienten in der mitte ein (auch in die gleiche richtung) zeigendes homogenes Magnetfeld mit blende in der mitte und einem hochfrequenzfeld | |||
*ausnutzung des zeemann effekt (spin bahn kopplung) für die inhomogenen magnefeldstrecken | |||
*spin umkehr bei passender hf | |||
*passieren des aufbaus nur bei spinumkehr in der mitte möglich | |||
===Dopplerfreie Laserspektroskopie=== | |||
*<math>h\nu</math> reicht nur aus für 2 Photonen, also hin und rückweg somit wird dopplereffekt kompensiert | |||
===Mößbauer Effekt=== | |||
*rückstoßfreie Emission oder Absorption von <math>\gamma</math>-Strahlung durch einen Atomkern | |||
[[File:Zeeman p s doublet.svg|miniatur|hochkant=2]] | |||
[[File:Zeeman p s doublet.svg]] | ===Prüfungsfragen=== | ||
*Rabi Experiment (Wunschthema) | |||
**Rabi -Experiment zur Messung des gyromagnetischen Verhältnisses (ausführlich erklärt). | |||
**was ist die Lamorfrequenz, warum präzidiert Drehimpuls-> Heisenbergsche Unschärferelation, keine gleichzeitige scharfe Messung von Iz, Ix und Iy. | |||
**Wie kann man Kernspins messen? -> Laserspektroskopie der HFS | |||
**Welche Größenordnung hat HFS? -> MHz- Ghz | |||
**Wie noch?-> Kernspinresonanzmethode-> Bestimmung der Lamorfrequenz | |||
**Wie kommt man da auf den Spin?-> Differenzmessung der Lamorfrequenzen, dadurch fallen konstante Faktoren raus. ( Wusste ich nicht) | |||
Aktuelle Version vom 28. August 2011, 22:47 Uhr

|
Der Artikel Messung von Kernmomenten basiert auf der Vorlesungsmitschrift von Moritz Schubotz des 6.Kapitels (Abschnitt 0) der Kern- und Strahlungsphysikvorlesung von Prof. Dr. P. Zimmermann. |
|}}
Die Abfrage enthält eine leere Bedingung.
Die Messung von Kernmomenten geschieht durch die Messung von Energieaufspaltungen, die durch die Wechselwirkung der Kernmomente mit
äußeren oder inneratomaren elektromagnetischen Feldern verursacht werden.
äußere Felder: Kernspinresonanzmethode
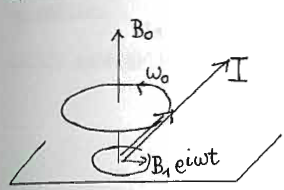
Größenordnung
Zusätzliches zirkulares Wechselfeld induziert Übergänge für
ANMERKUNG Schubotz:
|
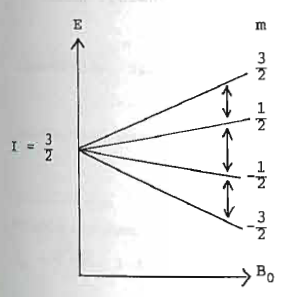
induzierte Absorption und Emission: Netto-Energieübertrag nur bei unterschiedlicher Besetzung der Zeemanniveaus durch Boltzmann-Verteilung im Festkörper.
| ANMERKUNG Schubotz: Ist im Umkehrschluss auch eine Temperaturmessung durch Kernspinausrichtung möglich? |
Messung des Kernspins
Einschub: Gehört nicht zum Skript (möglicherweise Fehlerbehaftet) Aus Skript von A.Voßkühler
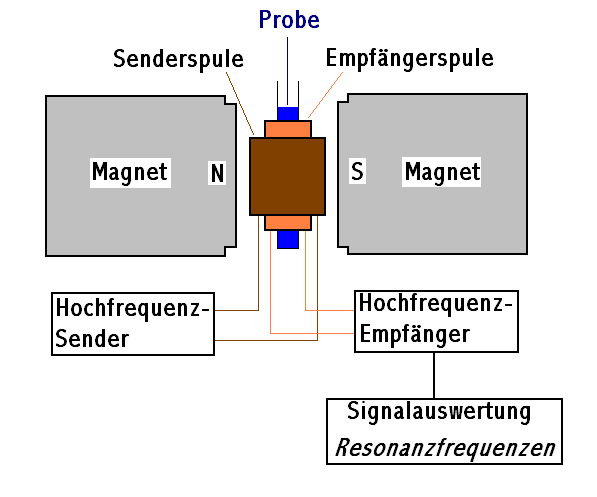
Die Probe, die aus vielen Atomen bzw. Molekülen bestehen kann, wird in ein externes homogenes Magnetfeld gegeben. Für die Untersuchung eignen sich alle Atomkerne, die ein Kernspin aufweisen. Liegt ein externes Magnetfeld an (in z-Richtung), richten sich die Kernspins nach diesem Magnetfeld aus, da sie dann die geringste potentielle Energie besitzen. Durch die thermische Energie der Atome sind die Kernspins nach der Maxwell- Boltzmann- Verteilung ausgerichtet, mit einer Vorzugsrichtung parallel zum Magnetfeld. Damit ergibt sich eine durchschnittliche Magnetisierung, die aufgrund der Maxwell- Boltzmann- Verteilung bei Raumtemperatur sehr klein ist. In der x/y-Ebene sind eine oder mehrere Spulen angeordnet, mit denen auf die Probe elektromagnetische Wechselfelder eingestrahlt werden (Sendespule) oder mit denen solche Felder empfangen werden (Empfangsspule). Durch die Sendespule wird ein starkes, zeitlich kurzes Magnetfeld aufgebaut, welches senkrecht zum externen Magnetfeld liegt. Die Spins richten sich an dem neuen Magnetfeld aus und kippen mit der Relaxationszeit in die x/y- Ebene. Die Dauer des Pulses bestimmt den Winkel, um den die Kernspins gekippt werden.
Wird die Sendespule ausgeschaltet, liegt wieder das normale Magnetfeld vor. In diesem Magnetfeld präzedieren die Spins mit der Larmorfrequenz, bis sich diese nach einer Relaxationszeit wieder nach dem Magnetfeld ausrichten. Die präzedierenden Spins induzieren in der Empfangsspule eine Wechselspannung mit der Larmorfrequenz, die dann analysiert wird.
CW-Verfahren
Hier wird die eingestrahlte Radiofrequenz langsam durchgestimmt und die Absorption der Strahlung gemessen. Man arbeitet in der Frequenzdomäne und erhält zunächst ein Absorptionsspektrum als Funktion der Frequenz. Die Probe wird mit einem extrem schmalen Signal angeregt.
Puls-Verfahren
Hierbei wird ein einzelner Radiofrequenzimpuls auf die Probe gesandt, die sich in der Spule befindet. Da der kurze Puls relativ breitbandig ist, werden mit einem Puls viele einzelne Resonanzen angeregt. Das Signal nach einem Puls oder das Spin-Echo nach zwei oder mehreren Impulsen, wird als Funktion der Zeit registriert. Mittels Fourier- Transformation wird das Zeitsignal in ein Spektrum umgewandelt.
Messung
Die Larmorfrequenz des Atoms ist stark von dem lokalen Magnetfeld abhängig. Da alle Atome unterschiedliche Magnetfelder besitzen, ist die Larmorfrequenz des untersuchten Atoms stark von der chemischen Umgebung und von der Bindung abhängig. Durch die Bestimmung der daraus resultierenden chemischen Verschiebung lassen sich Rückschlüsse auf die Bindungspartner und Arten der Bindungen ziehen. Die Stärke und die Verteilung mehrerer Resonanzen erlaubt Rückschlüsse auf die Dichte des Atomes mit einer bestimmten chemischen Verschiebung in der Probe. Die Aufspaltungen der Peaks lassen Rückschlüsse über Wechselwirkungen mit benachbarten Atomgruppen zu. (Singulett s: keine Aufspaltung, 1 Peak , Duplett d: Aufspaltung in 2 Peaks usw.) Probleme Durch die Boltzmannverteilung tragen nur wenige Spins zur Magnetisierung und damit zum messbaren Signal bei. Deswegen sind konventionelle NMR-Messungen nur für Flüssigkeiten oder Festkörper ausgelegt. Für vernünftige Messungen an einer Atomsorte ist mindestens 1 mol notwendig.
Noch einmal anders
Unter äußerem Magnetfeld spalten die Kernspins boltzmannverteilt auf. Die meisten Kernspins sitzen unten parallel zu B. Durch eine Energie in Form von Sendemagnetfeld mit Larmorfrequenz entsprechend dem ∆E = ϖL können Spins umgeklappt werden, was das magnetische Moment des Stoffes ändert und damit eine Spannung induziert. Möchte man stärkere Effekte haben, muss man die Besetzungsdifferenz erhöhen, d.h. noch tiefere Temperaturen oder größere Magnetfelder. Außerdem hilft eine möglichst große Anzahl von Atomen oder Molekülen.
Ende Einschub
inneratomare Felder der Hüllenelektronen
Hyperfeinstrukturaufspaltung durch Kopplung von
- Hüllendrehimpuls und
- Kernspin zu einem
- Gesamtdrehimpuls
| ANMERKUNG Schubotz: E steht für Energie (Schrödingergleichung und nicht für das elektrische Feld |
Größenordnung inneratomarer B-Felder der Valenzelektronen etwa
- 2. elektrische, HFS
- Wechselwirkung des elektrischen Kernquadrupolmoments mit dem
- elektrischen Feldgradienten der Hüllenelektronen (WW von Tensoren 2. Stufe)
Messung der HFS-Aufspaltung durch optische Methoden (z.B. dopplerfreie Laserspektroskopie, Doppelresonanz, Level-Crossing, Rabiatomstrahlresonanzmethode, Mößbauereffekt, etc.)
Weitere Informationen
(gehört nicht zum Skript)
Rabi-Experiment
- Aufbau:Zwei inhomogene magnetfelder mit gleicher feldaurichtung aber entgegengesetztem feldgradienten in der mitte ein (auch in die gleiche richtung) zeigendes homogenes Magnetfeld mit blende in der mitte und einem hochfrequenzfeld
- ausnutzung des zeemann effekt (spin bahn kopplung) für die inhomogenen magnefeldstrecken
- spin umkehr bei passender hf
- passieren des aufbaus nur bei spinumkehr in der mitte möglich
Dopplerfreie Laserspektroskopie
Mößbauer Effekt

Prüfungsfragen
- Rabi Experiment (Wunschthema)
- Rabi -Experiment zur Messung des gyromagnetischen Verhältnisses (ausführlich erklärt).
- was ist die Lamorfrequenz, warum präzidiert Drehimpuls-> Heisenbergsche Unschärferelation, keine gleichzeitige scharfe Messung von Iz, Ix und Iy.
- Wie kann man Kernspins messen? -> Laserspektroskopie der HFS
- Welche Größenordnung hat HFS? -> MHz- Ghz
- Wie noch?-> Kernspinresonanzmethode-> Bestimmung der Lamorfrequenz
- Wie kommt man da auf den Spin?-> Differenzmessung der Lamorfrequenzen, dadurch fallen konstante Faktoren raus. ( Wusste ich nicht)