Das Schalenmodell des Kerns: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
|||
| (6 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
<noinclude>{{ScriptProf|Kapitel=7|Abschnitt=0|Prof=Prof. Dr. P. Zimmermann|Thema=Kern- und Strahlungsphysik|Schreiber=Moritz Schubotz}}</noinclude> | <noinclude>{{ScriptProf|Kapitel=7|Abschnitt=0|Prof=Prof. Dr. P. Zimmermann|Thema=Kern- und Strahlungsphysik|Schreiber=Moritz Schubotz}}</noinclude> | ||
Ausgangspunkt: Das Auftreten besonders stabiler Nukleonenkonfiguration | |||
mit charakteristischen Sprüngen in der Separationsenergie bei den | mit charakteristischen Sprüngen in der Separationsenergie bei den sogenannten {{FB|magischen Zahlen}} | ||
Atomhülle. Deshalb als Wiederholung: | :<math>N, Z = 2, 8, 20, 28, 50, 82, 126</math> | ||
(N) in großer Ähnlichkeit mit den Edelgaskonfigurationen der Atomhülle. Deshalb als Wiederholung: | |||
:'''Atomhülle''' | |||
[[Datei:AtomhuelleNieveau24.png]] | [[Datei:AtomhuelleNieveau24.png|miniatur|hochkant=3|zentriert|Edelgaskonfiguration der Atomhülle{{AnMS|Ry ist wahrscheinlich <math>R_\infty</math>]] | ||
Aufhebung der {{FB|l-Entartung}}, d-Elektronen (Übergangsmetalle) und f-Elektronen (Lanthaniden, Aktiniden) werden "zu spät" eingebaut. | |||
Schalenabschlüsse bei den Edelgasen | |||
:<math>z = 2, 10, 18, 36, 54, 86</math> als den '''magischen Zahlen der Atomhülle'''. | |||
'''Aufgabe für die Kernphysik:''' Ein Zentralpotential so zu wählen, dass bei den '''Schalenabschlüssen''' die magischen Zahlen erscheinen. | |||
Wegen rechnerischer Einfachheit werden oft das {{FB|Kastenpotential}} oder das {{FB|0szillatorpotential}} benutzt. | |||
rechnerischer Einfachheit werden oft das Kastenpotential oder das | |||
[[Datei:KastenOszillatropotential25.png|miniatur|hochkant=3|zentriert|Kastenpotential]] | |||
Da es zunächst nur auf die relative Reihenfolge der Energieniveaus ankommt, kann man die Potentiale nach <math>\infty</math> fortsetzen. | |||
Da es zunächst nur auf die relative Reihenfolge der | |||
ankommt, kann man die Potentiale nach <math>\infty</math> fortsetzen. | |||
Ergebnis z.B. für das Oszillatorpotential: | Ergebnis z.B. für das Oszillatorpotential: | ||
:Äquidistante Abstände der Energieniveaus mit l-Entartung, die bei dem "abgeschnittenen" Potential aufgehoben wird. | |||
[[Datei:Aufhebung_l-entartung26.png|miniatur|hochkant=3|zentriert|Ergebnis z.B. für das Oszillatorpotential]] | |||
Ebenso wie hier werden auch beim Kastenpotential und selbst für realistische Potentialformen wie das {{FB|Wood-Saxon-Potential}} nur die ersten drei magischen Zahlen als Schalenabschlüsse erreicht. | |||
Lösung: Zusätzliche (starke) {{FB|Spin-Bahn-Kopplung}} | |||
;Goeppert-Mayer <ref>Goeppert-Mayer: Phys. Rev. 75, 1969 (49) </ref> | |||
;Haxel , Jensen, Suess: <ref>Haxel, Jensen, Suess:Phys. Rev. 75, 1966 (49)</ref> | |||
; | |||
: <math>V = V(r) + V_{SB} (ls)</math>, <math>|V_{SB}|\approx 1-2 MeV, V_{SB}<0 </math> attraktiv | : <math>V = V(r) + V_{SB} (ls)</math>, <math>|V_{SB}|\approx 1-2 MeV, V_{SB}<0 </math> attraktiv | ||
{{FB|Dublettaufspa1tung}}: | |||
<math>\begin{align} | <math>\begin{align} | ||
\vec l \vec s= & \frac{1}{2}\left( \vec j^{2}- \vec l^{2}- \vec S^{2}\right)\\ | |||
\Rightarrow & \frac{1}{2}\left(j(j-1)-l(l+1)-\frac{3}{4}\right)\\ | \Rightarrow & \frac{1}{2}\left(j(j-1)-l(l+1)-\frac{3}{4}\right)\\ | ||
= & \frac{1}{2}l\quad\text{fuer}\quad j=l+{\frac{1}{2}}\\ | = & \frac{1}{2}l\quad\text{fuer}\quad j=l+{\frac{1}{2}}\\ | ||
| Zeile 58: | Zeile 48: | ||
[[Datei:Feinstruktur29.png]] | [[Datei:Feinstruktur29.png|miniatur|hochkant=3|zentriert|]] | ||
[[Datei:KernSchalenModell50-30.png]] | [[Datei:KernSchalenModell50-30.png|miniatur|hochkant=3|zentriert|]] | ||
=== Verbesserungen des reinen Schalenmodells === | === Verbesserungen des reinen Schalenmodells === | ||
Hinzunahme der Paarungskraft (bei Weizsäckerformel phänomenologisch als Paarungsterm <math>\delta \approx 1 -2 MeV</math> eingeführt) als ( | Hinzunahme der {{FB|Paarungskraft}} (bei Weizsäckerformel phänomenologisch als Paarungsterm <math>\delta \approx 1 -2 MeV</math> eingeführt) als (kurzreichweitige) Teil der "Restwechselwirkung", die das Bestreben hat, | ||
einen '''möglichst guten Überlapp''' der Nukleonenwellenfunktionen zu | |||
einen möglichst guten Überlapp der Nukleonenwellenfunktionen zu | |||
erzielen. Dies gelingt besonders gut durch "Antiparallelstellung" | erzielen. Dies gelingt besonders gut durch "Antiparallelstellung" | ||
der Einzeldrehimpulse und bewirkt den verschwindenden Kerndrehimpuls I = 0 aller (g, g)-Kerne im Grundzustand. | der Einzeldrehimpulse und bewirkt den '''verschwindenden Kerndrehimpuls''' <math>I = 0</math> aller (g, g)-Kerne im Grundzustand. | ||
[[Datei:UeberlagerungKerndrehimpulse-31.png]] | [[Datei:UeberlagerungKerndrehimpulse-31.png|miniatur|hochkant=3|zentriert|Überlapp der Nukleonenwellenfunktionen]] | ||
Damit wird für (u, g)- und (g, u)-Kerne der Kerndrehimpuls I = j | Damit wird für (u, g)- und (g, u)-Kerne der Kerndrehimpuls <math>I = j</math> des '''letzten ungepaarten Nukleons'''. Diese Regel stimmt für (fast) | ||
des letzten ungepaarten Nukleons. Diese Regel stimmt für (fast) | alle (u, g)- und (g, u)-Kerne, wobei allerdings zu berücksichtigen ist, daß die Paarungskraft die Reihenfolge innerhalb einer Schale | ||
alle (u, g)- und (g, u)-Kerne, wobei allerdings zu berücksichtigen | verändern kann, indern sie besonders große Einzeldrehimpulse <math>j</math> möglichst paarweise absättigt, so daß hohe Gesamtdrehimpulse <math>I</math> | ||
ist, daß die Paarungskraft die Reihenfolge innerhalb einer Schale | |||
verändern kann, indern sie besonders große Einzeldrehimpulse j | |||
möglichst paarweise absättigt, so daß hohe Gesamtdrehimpulse I | |||
nicht so häufig vorkommen. | nicht so häufig vorkommen. | ||
Eine weitere Verbesserung ist für Kerne zwischen den magischen zahlen mit großen Quadrupolmomenten (z.B. im Bereich der Seltenen Erden) die Verwendung eines ''''deformierten' Potentials''' <math>V = V(r, \theta)</math> {{FB|Nilsson-Modell}}. | |||
[[Datei:DeformiertesPotential32.png|miniatur]] | |||
[[Datei:DeformiertesPotential32.png|miniatur] | |||
Für das deformierte Potential ist der | Für das deformierte Potential ist der | ||
Bahndrehimpuls l und damit auch <math>j= | Bahndrehimpuls <math>\vec l</math> und damit auch <math>\vec j=\vec l+\vec s</math> | ||
keine Konstante der Bewegung mehr. Nur | ''keine'' Konstante der Bewegung mehr. | ||
die Projektion m auf die | Nur die Projektion <math>m</math> auf die Symmetrieachse bleibt konstant, wobei es zu einer Energieaufspaltung bezüglich | ||
der verschiedenen <math>m</math> kommt, je nachdem <math>j</math> die "Bahn" <math>1</math> mehr oder weniger lang <math>m</math> im Bereich des anziehenden Potentials verläuft. | |||
einer Energieaufspaltung bezüglich | |||
der verschiedenen m kommt, je nachdem j die "Bahn" 1 mehr oder weniger lang m | |||
im Bereich des anziehenden Potentials verläuft. | |||
Für '''angeregte''' Kernzustände ist die Einteilchenvorstellung eines | Für '''angeregte''' Kernzustände ist die Einteilchenvorstellung eines | ||
"Valenznukleons" nur sehr bedingt verwendbar. Am besten geht es | "Valenznukleons" nur sehr bedingt verwendbar. Am besten geht es | ||
noch ganz in der Nähe der magischen Zahlen, | noch ganz in der Nähe der magischen Zahlen, z.B. bei | ||
:<math>^{209}_{82}Pb \hat {=} \textrm{''} {}^{208}_{82}Pb \textrm{''} + (2g_{9/2})-</math>Valenzneutronen mit <math>^{208}_{82}Pb</math> doppelmagischer Rumpf | |||
z.B. bei <math>^{209}_{82}Pb \hat {=} \textrm{''} {}^{208}_{82}Pb \textrm{''} + (2g_{9/2})-</math>Valenzneutronen mit <math>^{208}_{82}Pb</math> doppelmagischer Rumpf | |||
| Zeile 109: | Zeile 86: | ||
Besonders zwischen den magischen Zahlen treten Anregungsspektren | Besonders zwischen den magischen Zahlen treten Anregungsspektren | ||
auf, die sehr viel besser durch '''kollektive''' Nukleonenbewegungen, z.B. | auf, die sehr viel besser durch '''kollektive''' Nukleonenbewegungen, z.B. | ||
durch Rotations- und Vibrationszustände - ähnlich wie bei | durch '''Rotations'''- und '''Vibrationszustände''' - ähnlich wie bei Molekülspektren - beschrieben werden können. Im Gegensatz zu den Molekülspektren sind die Verhältnisse jedoch weitaus komplizierter, da | ||
die Trennung in Einteilchenzustände, Vibrationen und Rotationen | die Trennung in Einteilchenzustände, Vibrationen und Rotationen | ||
keine gute Näherung darstellt, da die Bedingung E (Einteilchen) | keine gute Näherung darstellt, da die Bedingung | ||
E (Vibration) | :<math>\rm E (Einteilchen) \gg E (Vibration) \gg E (Rotation)</math> im Kern nur '''sehr schlecht''' erfüllt ist. | ||
ist. | {{AnMS|Die starke WW im Kern ist viel größer als die elektromagnetische WW in der Hülle}} | ||
==Einzelnachweise== | |||
<references /> | |||
==Ergänzende Informationen== | |||
(gehört nicht zum Skript) | |||
===Prüfungsfragen=== | |||
* Schalernnodell (Wood-Saxon-Potential, Spin-Bahn-Kopplung(Goeppert Mayer, vgl. Atomhülle), Magische Zahlen bis 28 aufmalen können) | |||
** Grenzen des Modells (Valenznukleonen, uu-Kerne werden schlecht beschrieben) | |||
** Kollektive Anregungen | |||
** Deformationen des Kerns -> Quadrupoltenne (Energieaufspaltung messbar mit dEldx) | |||
** Nielssonmodell (Aufhebung der rn-Entartung, ansonsten nichts genaueres) | |||
* Heutige Experimente und Theorien der Kerne (hier wollte sie, glaube ich, die Verbindung zwischen Streuexperimenten und theoretischen Modellentwickhmgen wissen) | |||
*Woher kommt das Geraffel am Anfang der Bindungsenergiekurve E_B/A(A)?->Schalenabschlüsse | |||
*Schalenmodell: erst nur harmonischer Oszillator dann Spinbahnterm zur Erklärung der magischen Zahlen. | |||
Aktuelle Version vom 28. August 2011, 13:51 Uhr

|
Der Artikel Das Schalenmodell des Kerns basiert auf der Vorlesungsmitschrift von Moritz Schubotz des 7.Kapitels (Abschnitt 0) der Kern- und Strahlungsphysikvorlesung von Prof. Dr. P. Zimmermann. |
|}}
Die Abfrage enthält eine leere Bedingung.
Ausgangspunkt: Das Auftreten besonders stabiler Nukleonenkonfiguration mit charakteristischen Sprüngen in der Separationsenergie bei den sogenannten magischen Zahlen
(N) in großer Ähnlichkeit mit den Edelgaskonfigurationen der Atomhülle. Deshalb als Wiederholung:
- Atomhülle

Aufhebung der l-Entartung, d-Elektronen (Übergangsmetalle) und f-Elektronen (Lanthaniden, Aktiniden) werden "zu spät" eingebaut. Schalenabschlüsse bei den Edelgasen
Aufgabe für die Kernphysik: Ein Zentralpotential so zu wählen, dass bei den Schalenabschlüssen die magischen Zahlen erscheinen.
Wegen rechnerischer Einfachheit werden oft das Kastenpotential oder das 0szillatorpotential benutzt.
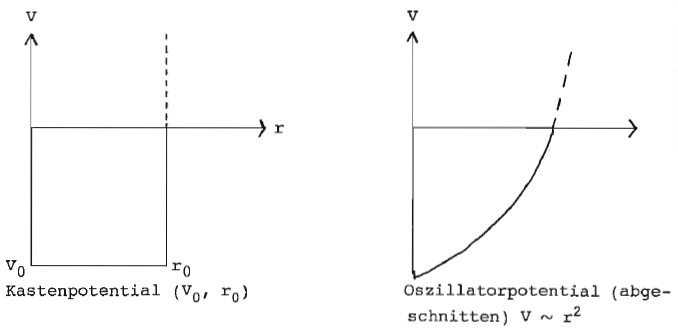
Da es zunächst nur auf die relative Reihenfolge der Energieniveaus ankommt, kann man die Potentiale nach fortsetzen.
Ergebnis z.B. für das Oszillatorpotential:
- Äquidistante Abstände der Energieniveaus mit l-Entartung, die bei dem "abgeschnittenen" Potential aufgehoben wird.

Ebenso wie hier werden auch beim Kastenpotential und selbst für realistische Potentialformen wie das Wood-Saxon-Potential nur die ersten drei magischen Zahlen als Schalenabschlüsse erreicht.
Lösung: Zusätzliche (starke) Spin-Bahn-Kopplung
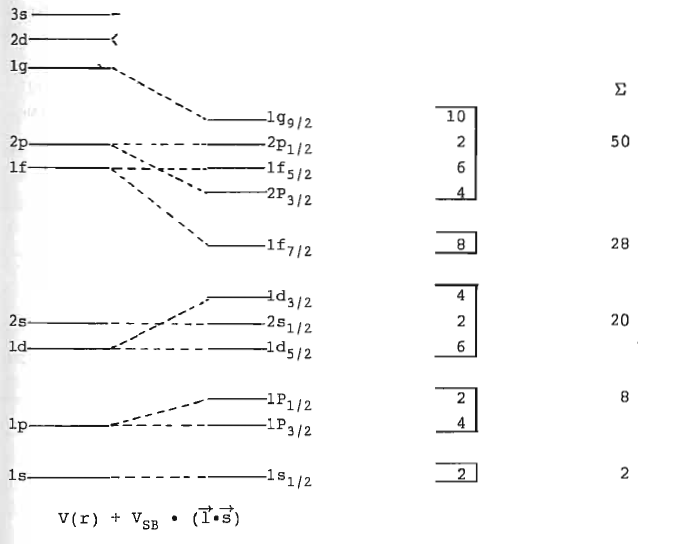
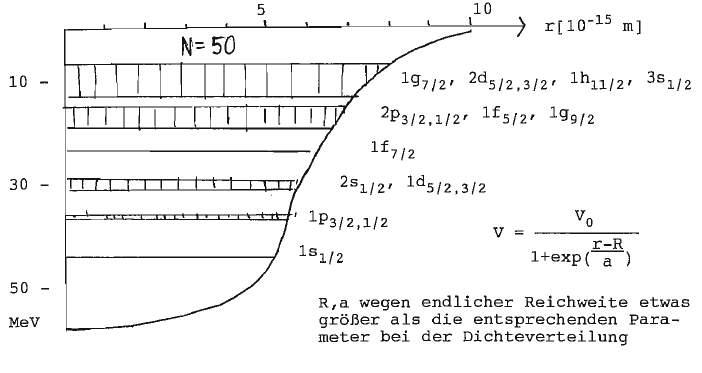
Verbesserungen des reinen Schalenmodells
Hinzunahme der Paarungskraft (bei Weizsäckerformel phänomenologisch als Paarungsterm eingeführt) als (kurzreichweitige) Teil der "Restwechselwirkung", die das Bestreben hat, einen möglichst guten Überlapp der Nukleonenwellenfunktionen zu erzielen. Dies gelingt besonders gut durch "Antiparallelstellung" der Einzeldrehimpulse und bewirkt den verschwindenden Kerndrehimpuls aller (g, g)-Kerne im Grundzustand.
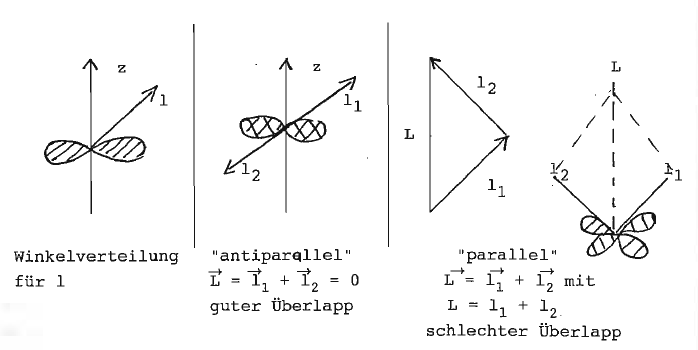
Damit wird für (u, g)- und (g, u)-Kerne der Kerndrehimpuls des letzten ungepaarten Nukleons. Diese Regel stimmt für (fast)
alle (u, g)- und (g, u)-Kerne, wobei allerdings zu berücksichtigen ist, daß die Paarungskraft die Reihenfolge innerhalb einer Schale
verändern kann, indern sie besonders große Einzeldrehimpulse möglichst paarweise absättigt, so daß hohe Gesamtdrehimpulse
nicht so häufig vorkommen.
Eine weitere Verbesserung ist für Kerne zwischen den magischen zahlen mit großen Quadrupolmomenten (z.B. im Bereich der Seltenen Erden) die Verwendung eines 'deformierten' Potentials Nilsson-Modell.
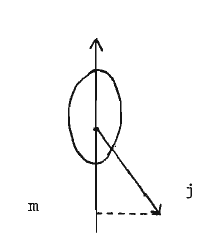
Für das deformierte Potential ist der Bahndrehimpuls und damit auch keine Konstante der Bewegung mehr. Nur die Projektion auf die Symmetrieachse bleibt konstant, wobei es zu einer Energieaufspaltung bezüglich der verschiedenen kommt, je nachdem die "Bahn" mehr oder weniger lang im Bereich des anziehenden Potentials verläuft.
Für angeregte Kernzustände ist die Einteilchenvorstellung eines "Valenznukleons" nur sehr bedingt verwendbar. Am besten geht es noch ganz in der Nähe der magischen Zahlen, z.B. bei
Besonders zwischen den magischen Zahlen treten Anregungsspektren auf, die sehr viel besser durch kollektive Nukleonenbewegungen, z.B. durch Rotations- und Vibrationszustände - ähnlich wie bei Molekülspektren - beschrieben werden können. Im Gegensatz zu den Molekülspektren sind die Verhältnisse jedoch weitaus komplizierter, da die Trennung in Einteilchenzustände, Vibrationen und Rotationen keine gute Näherung darstellt, da die Bedingung
| ANMERKUNG Schubotz: Die starke WW im Kern ist viel größer als die elektromagnetische WW in der Hülle |
Einzelnachweise
Ergänzende Informationen
(gehört nicht zum Skript)
Prüfungsfragen
- Schalernnodell (Wood-Saxon-Potential, Spin-Bahn-Kopplung(Goeppert Mayer, vgl. Atomhülle), Magische Zahlen bis 28 aufmalen können)
- Grenzen des Modells (Valenznukleonen, uu-Kerne werden schlecht beschrieben)
- Kollektive Anregungen
- Deformationen des Kerns -> Quadrupoltenne (Energieaufspaltung messbar mit dEldx)
- Nielssonmodell (Aufhebung der rn-Entartung, ansonsten nichts genaueres)
- Heutige Experimente und Theorien der Kerne (hier wollte sie, glaube ich, die Verbindung zwischen Streuexperimenten und theoretischen Modellentwickhmgen wissen)
- Woher kommt das Geraffel am Anfang der Bindungsenergiekurve E_B/A(A)?->Schalenabschlüsse
- Schalenmodell: erst nur harmonischer Oszillator dann Spinbahnterm zur Erklärung der magischen Zahlen.