Neutrinoexperimente: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
|||
| (14 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 5: | Zeile 5: | ||
== Rückstoßexperimente== | == Rückstoßexperimente== | ||
Am besten {{FB|Elektroneneinfang}} wegen {{FB|2-Körperproblem}}, gut geeignet z.B. | |||
e- + | :<math>e^- + {}^{37}\text{Ar}\underset{35d}{\to} {}^{37}Cl + \nu</math> (freies Edelgasatom in einer Gaszelle) mit <math>E_\nu = 810keV</math> | ||
Rückstoßenergie durch Flugzeitmessung: Rückstoßgeschwindigkeit v: | Rückstoßenergie durch Flugzeitmessung: Rückstoßgeschwindigkeit v: | ||
Mv = | <math>Mv = P_\nu = E_\nu/c, v/c = E_\nu/Mc^2= 8,1\times10^5 eV/37\times10^9 eV \approx 2\times10^{-5}\to v = 6\times10^5 cm/s</math> | ||
= 8, | |||
v = | Exp. von Rodeback und Allen <ref>Phys. Rev. 86, 446 (1952) [http://prola.aps.org/abstract/PR/v86/i4/p446_1 Neutrino Recoils Following the Capture of Orbital Electrons in A<sup>37</sup>]</ref> durch Koinzidenz | ||
Exp. von | von dem schnellen {{FB|Augerelektronen}}signal (Startsignal) und | ||
von dem schnellen | dem (verzögerten) Ionensignal (<math>^{37}Cl^+</math>), das bei einer Wegstrecke von | ||
dem (verzögerten) Ionensignal ( | z.B. <math>l = 6 cm</math> eine Flugzeit von <math>t = l/v = 6 cm/6\times10^5 cm s^{-1} = 10 \mu s</math> | ||
z.B. | |||
benötigt. | benötigt. | ||
== Inverser ß-Zerfall == | == Inverser ß-Zerfall == | ||
aus p | aus <math>\begin{align} | ||
p & \to n+e^+ +\nu \\ | |||
Wirkungsquerschnitt für | \tilde \nu + p & \to n+e^+ | ||
( | \end{align}</math> inverser ß-Zerfall, <math>E_0\approx E_{\tilde \nu}</math> | ||
Bedeutung von | |||
{{FB|Wirkungsquerschnitt}} für <math>E_{\tilde \nu} \approx MeV \sigma \approx 10^{-48} m^2</math> | |||
(<math>\sigma ~E_{ \nu} ^2</math> z.B. <math>E_{ \nu} \approx GeV \to \sigma\approx 10^{-42} m^2</math>) | |||
Festkörper z.B. Wasser N( | |||
[[Datei:14.1.bedeutung.wirkungsquerschnitt.png|miniatur|hochkant=3|Bedeutung von <math>\sigma</math> ]] | |||
Festkörper z.B. Wasser <math>N(H_20) \approx 3\times 10^{22}</math> Mo1eküle / cm³ | |||
z.B. N | |||
9 | <math>\sigma Nl =</math> Wahrscheinlichkeit für eine Reaktion | ||
cm | |||
z.B. <math>N \approx 10^{23}</math> Kerne/cm³, Targetlänge 1 = gesamte Erde = 1,2 <math>10^9</math> cm | |||
:<math>\to \sigma Nl \approx 10^{-44} cm^2 10^{23} cm^{- 30} 1,2 \times 10^9 cm\approx 10^{-12}</math> | |||
==Starke Neutrinoguellen== | ==Starke Neutrinoguellen== | ||
=== Reaktor <math>\triangleq </math> Antineutrino-Quelle=== | === Reaktor <math>\triangleq </math> Antineutrino-Quelle=== | ||
Spaltprodukte wegen Neutronenüberschuß | Spaltprodukte wegen {{FB|Neutronenüberschuß}} <math>\beta^-</math>-Strahler, die {{FB|Antineutrino}}s emittieren. | ||
emittieren. | |||
Pro Spaltung ca.6 | Pro Spaltung ca.<math>6\bar \nu</math>, daraus '<math>\bar \nu</math>-Produktion aus Reaktorleistung berechenbar: | ||
Pro Spaltung | |||
Pro Spaltung wird ca. 200 MeV= 3,2 10<sup>-17</sup> MWs frei, d. h. bei Leistung <math>L =1 MW \to N(\bar\nu) = \frac{6\bar \nu1MW}{3,2\times 10^{-17}}\approx 2\times 10^{17}\bar \nu /s</math> | |||
wird ca. 200 MeV | |||
1 MW | |||
3,2 | |||
=== Sonne <math>\triangleq </math> Neutrinoquelle === | === Sonne <math>\triangleq </math> Neutrinoquelle === | ||
Da bei der Fusion aus H - | Da bei der {{FB|Fusion}} aus H --> He entsteht, müssen dabei ebenso {{FB|Neutrino}}s entstehen. | ||
entstehen. | Fusion: <math>2e^- + 4p \underset{\text{CN-Zyklus}}{\to}He^4 + 2\nu + \text{ca. 20 MeV}</math>, d.h. pro 10 MeV | ||
Fusion: 2e- + 4p CN- | Fusionsenergie entsteht ca. 1 <math>\nu</math>. | ||
Fusionsenergie entsteht ca. 1 | |||
Damit Neutrinofluß auf der Erde aus Solarkonstante umgerechnet: | Damit Neutrinofluß auf der Erde aus Solarkonstante umgerechnet: | ||
S = 1,4 kW/ | S = 1,4 kW/m² 1<math>\nu\approx</math> 10 MeV = 1,6 10<sup>-12</sup> Ws | ||
[[Datei:14.3.reaktorneutrinos.prinzip.png|miniatur|zentriert| | :<math>N(\nu) = \frac{1,4 \times 10^3 Wm^{-2}}{1,6 \times 10^{12} Ws/nu} = 8\times10^{14}\nu/m^2s</math> | ||
Erstes Experiment von Reines und Cowan <ref>Phys. Rev. 92, 830 (53)</ref> mit Reaktorantineutrinos. (Los Alamos) | |||
Das Meßprinzip beruht darauf, daß bei einer möglichen Reaktion <math>\bar \nu+p \to n + e^+</math> die beiden Vernichtungsquanten aus der Positronzerstrahlung <math>e^+ + e^- \to 2 \gamma</math> (<math>E_\gamma = 0,5 MeV</math>) und nach einer bestimmten Abbremszeit durch Neutroneneinfang von <math>{}^{113}Cd</math> mehrere <math>\gamma</math> aus dem Kaskadenzerfall | |||
des hochangeregten <math>{}^{114}Cd</math> (<math>E \approx 9 MeV</math>) in Mehrfachkoinzidenz gemessen werden. | |||
[[Datei:14.2.messung.reaktorneutrinos.png|miniatur|zentriert|hochkant=3|Experiment Neutrinomessung (Reines und Cowan)]] | |||
[[Datei:14.3.reaktorneutrinos.prinzip.png|miniatur|zentriert|hochkant=3|Schema Neutrinomessung]] | |||
Grobe Abschätzung der Zählrate: | Grobe Abschätzung der Zählrate: | ||
Fluß in ca. 1 m Abstand | <math>\sigma</math> (Reaktor-<math>\bar \nu</math>) <math>\approx 10^{-47}m^2</math>, Reaktor <math>L \approx 10 MW ~ 2\times10^{18}\bar \nu/s</math> | ||
Targetfläche F = 7,6 cm • 150 cm | Fluß in ca. 1 m Abstand <math>\theta \approx 10^{17}\bar \nu/m^2s</math>, | ||
Targetfläche F = 7,6 cm • 150 cm <math>\approx</math> 0,1 m², d. h. ca. <math>10^{16}\bar \nu/s</math> durch | |||
Target von ca. 2 m Länge. | Target von ca. 2 m Länge. | ||
Reaktionswahrscheinlichkeit | |||
Zählrate/s | Reaktionswahrscheinlichkeit <math>\sigma Nl \approx 10^{-47}m^2 10^{29}m^{-3}2m\approx 10^{-18}</math> | ||
Zählrate/s <math>\approx 10^{16}s^{-1} 10^{-18} \approx 10^{-2}s^{-1}</math> | |||
Großer Untergrund durch Reaktor und kosmische Strahlung. Erste Ergebnisse | Großer Untergrund durch Reaktor und kosmische Strahlung. Erste Ergebnisse | ||
in Zählrate/min: 2,55 ± 0,15 Reaktor an | in Zählrate/min: | ||
2,14 ± 0,13 Reaktor aus | *2,55 ± 0,15 Reaktor an | ||
0,41 ± 0,20/min | *2,14 ± 0,13 Reaktor aus | ||
---- | |||
Prinzip e- + | *0,41 ± 0,20/min | ||
<math>\nu \neq \bar \nu</math>-Experiment <ref>Davis et al., Phys. Rev. 97, 766 (1955)</ref> | |||
Prinzip<math> \begin{align} | |||
4000 1 | e^- + {}^{37}\text{Ar} & \to {}^{37}\text{Cl} + \nu\\ | ||
& \leftarrow \\ | |||
& \nleftarrow {}^{37}\text{Cl} + \underbrace{\bar \nu}_{\text{Reaktor}} | |||
\end{align}</math> | |||
4000 1 CC1<sub>4</sub> wurden 30-70 Tage mit Reaktor-<math>\bar\nu</math> bestrahlt und etwa gebildetes <math>^{37}</math>Ar durch Aktivitätsmessung gezählt --> <u>Negatives</u> Ergebnis | |||
==Einzelnachweise== | |||
<references/> | |||
==Ergänzende Infromationen== | |||
(gehört nicht zum Skript) | |||
===[http://www.physik.rwth-aachen.de/~stahl/Seminar/Kaufmann.pdf Seminarvortrag Experimenteller Neutrinonachweis und Helizität]=== | |||
*oben beschriebenes Experiment ist 3. Versuch (Savannah River Experiment) | |||
*1. Idee Atombombe | |||
*2. Idee Hanford-> zu großes Rauschen (kosmische Strahlung) | |||
*Cd = Cadmium | |||
===Prüfungsfragen (Prof. Kanngießer)=== | |||
* Neutrinoexperimente (habe alle relevanten Experimente aus dem Mayer-Kuckuk aufgezählt) | |||
* Experiment von Reines und Cowan näher erklären (Reaktionen aufmalen, | |||
**Warum Zeitdifferenz? ->Abbremszeit der Neutronen; | |||
**Warum NaJ als 'Y-Detektor? -> wegen benötigter Detektorgröße | |||
* Neutrinos: Was ist das wozu braucht man die (beim ß Zerfall)? Problem Energie + Impulserhal tung + Spin -> Erklärung es ex. ungeladenes Fermion | |||
** Nachweis? | |||
*** Direkt: Ar->CI Rückstoß messen (Mit Skizze + ausführlicher Erklärung)Indirekt: induzierter Protonzerfall , e+e-Annihilalion; Koinzidenz verzögert CdNeutronnachweis | |||
** Was misst man jeweils Neutrino/Antineutrino; Wo bekommt man sie her?--> Sonne/Kernreaktor | |||
**warum? -> Neutronenüberschuß der Spaltprodukte | |||
Aktuelle Version vom 28. August 2011, 17:13 Uhr

|
Der Artikel Neutrinoexperimente basiert auf der Vorlesungsmitschrift von Moritz Schubotz des 14.Kapitels (Abschnitt 0) der Kern- und Strahlungsphysikvorlesung von Prof. Dr. P. Zimmermann. |
|}}
Die Abfrage enthält eine leere Bedingung.
a) indirekt über Rückstoßkern b) direkt über inversen ß-Zerfall
Rückstoßexperimente
Am besten Elektroneneinfang wegen 2-Körperproblem, gut geeignet z.B.
Rückstoßenergie durch Flugzeitmessung: Rückstoßgeschwindigkeit v:
Exp. von Rodeback und Allen [1] durch Koinzidenz von dem schnellen Augerelektronensignal (Startsignal) und dem (verzögerten) Ionensignal (), das bei einer Wegstrecke von z.B. eine Flugzeit von benötigt.
Inverser ß-Zerfall
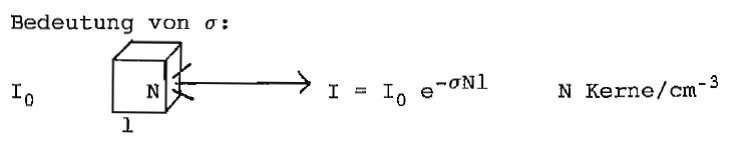
Festkörper z.B. Wasser Mo1eküle / cm³
Wahrscheinlichkeit für eine Reaktion
z.B. Kerne/cm³, Targetlänge 1 = gesamte Erde = 1,2 cm
Starke Neutrinoguellen
Reaktor Antineutrino-Quelle
Spaltprodukte wegen Neutronenüberschuß -Strahler, die Antineutrinos emittieren.
Pro Spaltung ca., daraus '-Produktion aus Reaktorleistung berechenbar:
Pro Spaltung wird ca. 200 MeV= 3,2 10-17 MWs frei, d. h. bei Leistung
Sonne Neutrinoquelle
Da bei der Fusion aus H --> He entsteht, müssen dabei ebenso Neutrinos entstehen. Fusion: , d.h. pro 10 MeV Fusionsenergie entsteht ca. 1 .
Damit Neutrinofluß auf der Erde aus Solarkonstante umgerechnet: S = 1,4 kW/m² 1 10 MeV = 1,6 10-12 Ws
Erstes Experiment von Reines und Cowan [2] mit Reaktorantineutrinos. (Los Alamos)
Das Meßprinzip beruht darauf, daß bei einer möglichen Reaktion die beiden Vernichtungsquanten aus der Positronzerstrahlung () und nach einer bestimmten Abbremszeit durch Neutroneneinfang von mehrere aus dem Kaskadenzerfall des hochangeregten () in Mehrfachkoinzidenz gemessen werden.
Grobe Abschätzung der Zählrate:
(Reaktor-) , Reaktor Fluß in ca. 1 m Abstand , Targetfläche F = 7,6 cm • 150 cm 0,1 m², d. h. ca. durch Target von ca. 2 m Länge.
Zählrate/s Großer Untergrund durch Reaktor und kosmische Strahlung. Erste Ergebnisse in Zählrate/min:
- 2,55 ± 0,15 Reaktor an
- 2,14 ± 0,13 Reaktor aus
- 0,41 ± 0,20/min
-Experiment [3]
4000 1 CC14 wurden 30-70 Tage mit Reaktor- bestrahlt und etwa gebildetes Ar durch Aktivitätsmessung gezählt --> Negatives Ergebnis
Einzelnachweise
- ↑ Phys. Rev. 86, 446 (1952) Neutrino Recoils Following the Capture of Orbital Electrons in A37
- ↑ Phys. Rev. 92, 830 (53)
- ↑ Davis et al., Phys. Rev. 97, 766 (1955)
Ergänzende Infromationen
(gehört nicht zum Skript)
Seminarvortrag Experimenteller Neutrinonachweis und Helizität
- oben beschriebenes Experiment ist 3. Versuch (Savannah River Experiment)
- 1. Idee Atombombe
- 2. Idee Hanford-> zu großes Rauschen (kosmische Strahlung)
- Cd = Cadmium
Prüfungsfragen (Prof. Kanngießer)
- Neutrinoexperimente (habe alle relevanten Experimente aus dem Mayer-Kuckuk aufgezählt)
- Experiment von Reines und Cowan näher erklären (Reaktionen aufmalen,
- Warum Zeitdifferenz? ->Abbremszeit der Neutronen;
- Warum NaJ als 'Y-Detektor? -> wegen benötigter Detektorgröße
- Neutrinos: Was ist das wozu braucht man die (beim ß Zerfall)? Problem Energie + Impulserhal tung + Spin -> Erklärung es ex. ungeladenes Fermion
- Nachweis?
- Direkt: Ar->CI Rückstoß messen (Mit Skizze + ausführlicher Erklärung)Indirekt: induzierter Protonzerfall , e+e-Annihilalion; Koinzidenz verzögert CdNeutronnachweis
- Was misst man jeweils Neutrino/Antineutrino; Wo bekommt man sie her?--> Sonne/Kernreaktor
- warum? -> Neutronenüberschuß der Spaltprodukte
- Nachweis?