Tröpfchenmodell, Weizsäckersche Massenformel

Kern- und Strahlungsphysikvorlesung von Prof. Dr. P. Zimmermann

Der Artikel Tröpfchenmodell, Weizsäckersche Massenformel basiert auf der Vorlesungsmitschrift von Moritz Schubotz des 4.Kapitels (Abschnitt 0) der Kern- und Strahlungsphysikvorlesung von Prof. Dr. P. Zimmermann.

   |}}

Die Abfrage enthält eine leere Bedingung.

Die nahezu konstante Nukleonendichte $\rho \approx 10^{17}kg/m^3$ und der nahezu konstante B/A-Wert ("Kondensationswärme") legt die Analogie zum Flüssigkeitstropfen nahe. Massenformel

Bindungsenergie setzt sich aus 5 Anteilen zusammen:

$B=\sum _{i=1}^5{B}_i$

1. Volumenenergie

$B_1=a_{1}A$ Volumenenergie ("Kondensationswärme" ) vermindert um

2. Oberflächenenergie

$B_2=-a_2{A}^{2/3}$ ~ Anzahl der Nukleonen an der

Oberfläche, die weniger stark gebunden sind.

3. Coulombenergie

$B_3=-\frac{1}{4\pi {ϵ}_0}\frac{5}{3}\frac{Z(Z-1)e^2}{R}=-a_3\frac{Z(Z-1)}{A^{1/3}}$ einer homogen geladenen Kugel

Durch die Coulombenergie $B_3$ würden für Isobare (A = const) zu stark Kerne mit vielen Neutronen bevorzugt. In Wirklichkeit ist jedoch $Z\approx N$.

Genauer: Nuklidkarte

Nuklidkarte

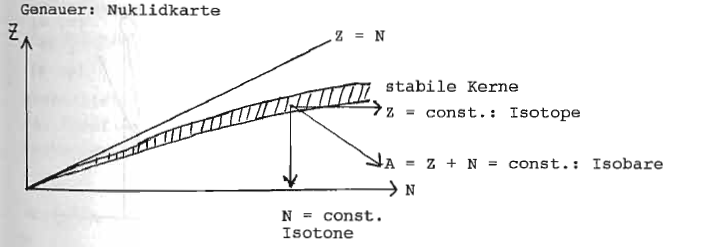
Als Gegengewicht genüber dem Coulombterm deshalb:

4. Asymmetrie-Energie

$B_4=-a_4\frac{(N-Z{)}^2}{A}$

Außerdem gilt folgende Regel, wenn man die Kerne bezüglich gerader oder ungerader Protonen- oder Neutronenzahl ordnet:

$\begin{array}{lllll}& (g,g)\to & (u,g),& (g,u)\to & (u,u)\to \text{Abnahme der Stabilitaet}\\ \text{stab}\text{. Kerne}& 158& 50,& 53& 6\\ \end{array}$

5. Parität

Deshalb $B_5=\delta =a_5{A}^{-1/2}$

mit $\begin{array}{rl}& \text{(g}\text{, g) : }\text{+}\delta \\ & \text{(u}\text{, g) }\text{, (g}\text{, u) : }\text{0}\\ & \text{(u}\text{, u) : }\text{-}\delta \\ \end{array}$

Anpassung der Formel an viele Massenwerte gibt einen optimalen Wertesatz für die 5 Parameter $a_i:a_1=16MeV,a_2=18MeV,a_3=0,7MeV,a_4=23MeV$ und mit $a_5=12MeV$ ). Genauigkeit $\approx 1\%ab\approx 40$.

Folgerungen aus der Weizsäckerschen Massenformel

I. Isobarenregeln

Für Isobare (A = const.) ist die Massenformel quadratisch in Z, deshalb bekommt man für A = ungerade, d.h. für (u, g)- und (g, u)-Kerne eine Parabel und für A = gerade, d.h. für (g, g)- und (u, u)-Kerne zwei Parabeln, die durch den Abstand $2\delta$ der Paarungsenergie $\delta$ getrennt sind.

Isobarenparabeln

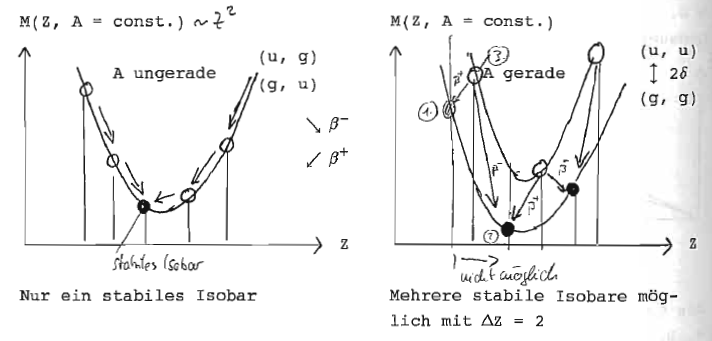
Trägt man die Massenwerte in die Nuklidkarte auf der N-Z-Ebene nach oben auf, dann sind die Isobarenparabeln Schnitte längs der Linie A = Z + N = const. Die stabilen Kerne liegen in der "Talsohle des Massetals".

Umwandlung durch Beta-Zerfall:

$\begin{array}{rl}{\beta }^{+}:n& \to p+e^{-}+\tilde{\nu }\\ {\beta }^{-}:n& \to p+e^{+}+\nu \\ e^{-}+p& \to n+\tilde{\nu }\\ \end{array}$ Konkurrenzprozeß: Kerneinfang

II. Kernspaltung und Fusion

Allgemein für leichtere Kerne Energiegewinn durch Fusion, für schwerere Kerne durch Spaltung möglich. Spontane Fusion durch Coulombabstoßung, spontane Spaltung durch Spaltschwelle behindert.

Spaltung

Stabilitätsbetrachtung bezüglich spontaner Spaltung

Coulombenergie

$B_3\to B_3(1-\frac{1}{5}ϵ{)}^2$ nimmt ab.

Oberflächenenergie

$B_2\to B_2(1+\frac{2}{5}ϵ{)}^2$ nimmt zu.

Stabilitätsbedingung gegenüber spontaner Spaltung: größere Zunahme der Oberflächenenergie als Abnahme der Coulombenergie.

Rechnung: $Z^2/A\lesssim 51$

Für $Z^2/A\lesssim 51$ Spaltschwelle:

Spaltschwelle

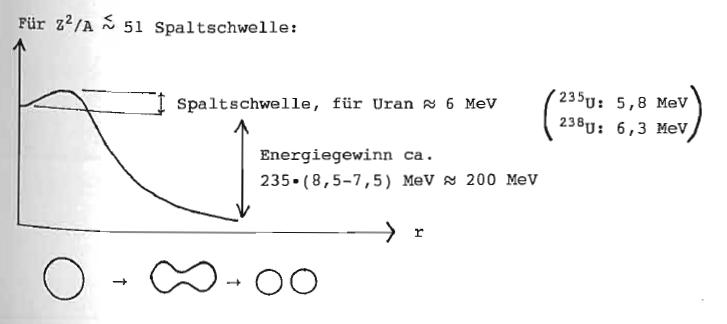
Neutroneninduzierte Spaltung bei Uran durch freiwerdende Bindungsenergie bei Neutroneneinfang. Für thermische Neutronen ist diese Bindungsenergie

bei ${235}^{}U+n{\to }^{236}U+6,4MeV(g,u)\underset{n}{\to }(g,g)$

bei ${238}^{}U+n{\to }^{239}U+4,8MeV(g,g)\underset{n}{\to }(g,u)$

Die fehlende Paarungsenergie bei ${239}^{}U$ bedingt die niedrigere Bindungsenergie, so daß bei ${238}^{}U$ der Einbau thermischer Neutronen nicht zur Überwindung der Spaltschwelle ausreicht.

Allgemein Spaltprozeß: ${235}^{}U+n\text{<mrow data-mjx-texclass="ORD"><mo stretchy="false">(</mo>thermisch<mo stretchy="false">)</mo></mrow>}{\to }^{236}U\to X+Y+kn$

Spaltbruchstücke X und Y instabil wegen Neutronenüberschuß, ${\beta }^{-}$-Zerfall, z.B.

instabile Spaltbruchstücke

Grobe Abschätzung für ${235}^{}U$-Verbrauch:

$1kg{}^{235}U:E=N\mathrm{\Delta }E\backsimeq \frac{1000}{235}6\times 10^{23}\times 2\times 10^8\times 1,6\times 10^{-19}Ws\backsimeq 8\times 10^{13}Ws\backsimeq 10^{8}MWd$

That’s more than snseblie! That’s a great post!

xAu9UT <a href="http://jwxdzufcycld.com/">jwxdzufcycld</a>