Kernradien: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
|||
| (12 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
<noinclude>{{ScriptProf|Kapitel=2|Abschnitt=0|Prof=Prof. Dr. P. Zimmermann|Thema=Kern- und Strahlungsphysik|Schreiber=Moritz Schubotz}}</noinclude> | <noinclude>{{ScriptProf|Kapitel=2|Abschnitt=0|Prof=Prof. Dr. P. Zimmermann|Thema=Kern- und Strahlungsphysik|Schreiber=Moritz Schubotz}}</noinclude> | ||
Kernradienbestimmung durch Streuexperimente mit hochbeschleunigten Elektronen ( | Kernradienbestimmung durch {{FB|Streuexperimente}} mit hochbeschleunigten Elektronen ({{FB|Hofstadter-Experiment}}e) | ||
[[Datei:Beugungsminimum3.png|miniatur|Hofstadter-Experimente]] | |||
Beugungsmaxima und -minima | Beugungsmaxima und -minima | ||
Erstes Minimum bei <math>\sin \theta \approx 0,61 \frac{\lambda}{d}</math> | Erstes Minimum bei <math>\sin \theta \approx 0,61 \frac{\lambda}{d}</math> | ||
Bedingung: <math>\lambda \le d</math> | Bedingung: <math>\lambda \le d</math> | ||
| Zeile 11: | Zeile 12: | ||
Für Kern <math>\lambda \le 10^{-14} m</math>, als 'Licht' sind hochbeschleunigte Elektronen gut geeignet (keine Starke WW). | Für Kern <math>\lambda \le 10^{-14} m</math>, als 'Licht' sind hochbeschleunigte Elektronen gut geeignet (keine Starke WW). | ||
Verknüpfung von Energie E, Impuls p und Wellenlänge <math>\lambda</math> durch relativistische Energiegleichung: | Verknüpfung von {{FB|Energie}} E, {{FB|Impuls}} p und {{FB|Wellenlänge}} <math>\lambda</math> durch {{FB|relativistische Energiegleichung}}: | ||
[[Datei:EnergieMasseEinstein4.png|miniatur|zentriert|hochkant=4|Einstein Energiegleichung]] | |||
Für relat. Teilchen (<math>E \gg m_0c^2</math>, exakt für Teilchen mit Ruhemasse <math>m_0= 0</math>, d.h. Photonen, Neutrinos (?), Gravitonen (?), ... ) gilt wegen <math>E = pc</math> für die de Broglie-Wellenlänge <math>\lambda\!\!\!{}^{-}</math>: | Für relat. Teilchen (<math>E \gg m_0c^2</math>, exakt für Teilchen mit Ruhemasse <math>m_0= 0</math>, d.h. Photonen, Neutrinos (?), Gravitonen (?), ... ) gilt wegen <math>E = pc</math> für die de Broglie-Wellenlänge <math>\lambda\!\!\!{}^{-}</math>: | ||
:<math>\lambda\!\!\!{}^{-}=\frac{\hbar}{p}=\frac{ | :<math>\lambda\!\!\!{}^{-}=\frac{\hbar}{p}=\frac{\hbar c}{E}\approx \frac{3\times 10^{8-34} m}{1.6\times 10^{-19+6} E[MeV]}\approx 200 \frac{10^{-15}}{E[MeV]}</math> | ||
d.h. für <math>E > 200 MeV</math> ist <math>\lambda\!\!\!{}^{-}< 10^{-15} m</math>. | d.h. für <math>E > 200 MeV</math> ist <math>\lambda\!\!\!{}^{-}< 10^{-15} m</math>. | ||
Hofstädter-Experimente am Linearbeschleuniger in Stanford 1957 (Zusammenfassend: Rev. Mod. Phys. 1Q, 142-584 (1958) http://rmp.aps.org/abstract/RMP/v30/i2/p412_1) | Hofstädter-Experimente am Linearbeschleuniger in Stanford 1957 <ref>(Zusammenfassend: Rev. Mod. Phys. 1Q, 142-584 (1958) http://rmp.aps.org/abstract/RMP/v30/i2/p412_1)</ref> | ||
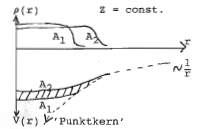
[[Datei:PraktischeAusfuehrungKernradius5.png|miniatur|zentriert|hochkant=3]] | |||
| Zeile 29: | Zeile 35: | ||
Für alle Kerne etwa gleiche | [[Datei:UnscharferKernrand6.png|gerahmt|zentriert|hochkant=4|Für alle Kerne etwa gleiche | ||
Ladungsdichte | Ladungsdichte <math>\rho_0</math> im Inneren | ||
und gleiche Randbreite von | und gleiche Randbreite von | ||
ca. <math>2\times10^{-15}</math> m. | ca. <math>2\times10^{-15}</math> m.]] | ||
Quantitativ beschreibbar durch die '''Wood-Saxon-Formel''':{{Gln| | |||
:<math>\rho(r) = \frac{\rho_0}{1+\exp{\frac{r-R}{a}}}</math> | :<math>\rho(r) = \frac{\rho_0}{1+\exp{\frac{r-R}{a}}}</math> | ||
|Wood-Saxon-Formel}} | |||
Randbreite (90% <math>\to</math> 10% Abfall) <math>\approx 4,40a \approx 2,4 \times10^{-15}m</math> | Randbreite (90% <math>\to</math> 10% Abfall) <math>\approx 4,40a \approx 2,4 \times10^{-15}m</math> | ||
| Zeile 45: | Zeile 51: | ||
Andere Meßmethoden zur Kernradienbestimmung: Isotopieverschiebung | Andere Meßmethoden zur Kernradienbestimmung: {{FB|Isotopieverschiebung}} | ||
( | (Volumeneffekt) im optischen Bereich | ||
besonders für S-Elektronen wegen | |||
[[Datei:Isotopenverschiebung7.png|miniatur|miniatur|zentriert|hochkant=4|besonders für S-Elektronen wegen | |||
deren endlicher Aufenthaltswahrscheinlichkeit | deren endlicher Aufenthaltswahrscheinlichkeit | ||
am Kernort. | am Kernort. | ||
Noch wesentlich stärkerer Effekt | Noch wesentlich stärkerer Effekt | ||
bei myonischen Atomen wegen der | bei myonischen Atomen wegen der | ||
ca. 200x kleineren Bahnradien. | ca. 200x kleineren Bahnradien.]] | ||
==Weitere Informationen== | |||
(gehört nicht zum Skript) | |||
[http://www.leifiphysik.de/web_ph12/umwelt_technik/11radien/elektronen.htm Hofstäder-Experiment] | |||
[[w:Hofstadter-Experiment]] | |||
===merken=== | |||
* Kernradius <math>R=r_0 \sqrt[3]{A}</math>, mit <math>r_0=(1,3\pm0,1) \text{fm}</math> | |||
* Masse <math>\sim A U (1 U =1m_u=\frac{1g}{N_A}=931MeV\frac{1}{c})</math> | |||
* Dichte ~ <math>10^{17} fm</math> | |||
* Randschärfe <math>a=0.55\text{fm}</math> | |||
* Messung von Kernradien <math>\frac{d\sigma}{d\Omega}=\left(\frac{ZZ'e^2}{4\pi\epsilon_0 4E}\right)^2\frac{1}{\sin^4\frac{\theta}{2}}=\frac{1}{4\pi\epsilon_0}\left(Z Z' 2m e^2 \right)^2\frac{1}{q^4}</math> | |||
* Erweiterung Mott Streuung mit <math>W^2=p^2c^2+m_0^2c^4</math> <math>\frac{d\sigma}{d\Omega}_{\text{Mott}}=\frac{1}{4\pi\epsilon_0}\left(Z Z' 2 W e^2 \right)^2\frac{1}{q^4c^4}\left[1-\frac{v}{c}\sin^2\frac{\theta}{2}\right]</math> Coulomb-Streuung von Elektronen (Spin <math>\frac{1}{2}</math> an spinlosem Target)) | |||
====3 Experimentelle Arten zur Bestimmung des Kernradius==== | |||
# Hofstädter Experiment | |||
<math>\frac{d\sigma}{d\omega}_{\text{Hof}}=\frac{d\sigma}{d\omega}_{\text{Punkt, Mott}}|F(q^2)|^2</math> | |||
mit <math>F(q)=\int d\vec r \rho(\vec r) \exp{\frac{i}{\hbar}\vec q \vec r}</math> {{Quelle|BS| Gleichung 4.15}} | |||
*Wood Saxon Formel | |||
*Geschwindigkeit >200 MeV mit De-Brogli Wellenlänge im fm Bereich | |||
# Myonische Atome | |||
# Isotopieverschiebung | |||
==Prüfungsfragen== | |||
* Äußere Eigenschaften eines Kerns | |||
** Masse | |||
** Randschärfe (vgl. Mit Atomhülle) | |||
*Rutherfordscher Steuversuch | |||
**Wie misst man Radius -> Streuexperimente (Rutherford erklärt) | |||
**Was ist der differentielle Wirkungsquerschnitt? | |||
**Was ist das für eine Größe? ->statistisch Abschätzung des Kernradius über kritischen Winkel, bei dem Abweichung vom Rutherfordstreuquerschnitt vorliegt. | |||
**Was für eine Streuung liegt vor?-> elastische Streuung | |||
**Was verändert sich bei inelastischer Streuung?->Energieübertrag an Target. | |||
**Warum Goldfolie und kein Gas? | |||
*Hofstädter Experiment | |||
**Was ändert sich bei Hofstädter Experiment? -> Wellenmechanische Beschreibung des Streuproblems. | |||
**Was wird gemessen?-> Ladungsverteilung. | |||
** Wie sehen Ladungsverteilungen (Protonverteilung) aus? | |||
**Wie sieht Neutronverteilung aus?-> Wood-Saxon Form aufmalen. Bei Protonen mit Anstieg beim Rand des Kerns. | |||
**Was ergibt sich für den Wirkungsquerschnitt für ein Bild-> Bild mit Beugungsminima | |||
***Warum?-> Analogie zur Beugung am Hindernis/Beugung am Einzelspalt. | |||
** Welche Energie haben die Elektronen?-> 200MeV | |||
** Warum?-> Damit Wellenlänge im fm-Bereich ist. | |||
**Wie berechnet man die Wellenlänge? -> de Brouglie: lambda=hquer / omega | |||
**Was für ein Beugungsbild bekommt man?-> Fraunhoferbeugung (Bild aufgemalt) | |||
**Wie bekommt man aus Streuwirkungsquerschnitt die Ladungsverteilung? ->Streuwirkungsquerschnitt=Rutherfordquerschnitt mal Formfaktor (Fouriertrafo der Ladungsverteilung) | |||
***Warum Formfaktor? | |||
****-> bei Rutherford wurde von Punktladung ausgegangen, hier ausgedehnte Ladungsverteilung. | |||
****-> Vorgehen Potential (Wood-Saxon-Form) raten und anpassen bis ermittelter Streuquerschnitt über Fouriertrafo der Ladungsverteilung und Rutherfordquerschnitt mit den Messwerten übereinstimmt. | |||
**Warum keine „Vorwärtsrechnung“ möglich? (Vergleich mit Atomphysik) -> Hier komplizierter, da kein Zentralpotential und Überlagerung verschiedener Kräfte (Coulomb, starke, schwache WW). | |||
**Kemradienmessung | |||
*** Rutherford -> Hofstädter (Formfaktor nur mit Leptonenstreuung, Mottstreuung erwähnt) | |||
***Myonisches Atom (nur erwähnt) | |||
**Wie misst man die Neutronenverteilung. daja vorherige Beispiele nur die Ladungsverteilung liefern? -> Streuung mit Hadronen wegen schwerer WW (z.B. a-Teilchen) | |||
[[File:Stanford-linear-accelerator-usgs-ortho-kaminski-5900.jpg|thumb|Stanford Linear Accelerator, shown in an aerial digital orthoimage. The two roads seen near the accelerator are California Interstate 280 (to the East) and Sand Hill Road (along the Northwest).]] | |||
==Literatur== | |||
<references /> | |||
Aktuelle Version vom 17. August 2011, 13:09 Uhr

|
Der Artikel Kernradien basiert auf der Vorlesungsmitschrift von Moritz Schubotz des 2.Kapitels (Abschnitt 0) der Kern- und Strahlungsphysikvorlesung von Prof. Dr. P. Zimmermann. |
|}}
Die Abfrage enthält eine leere Bedingung.
Kernradienbestimmung durch Streuexperimente mit hochbeschleunigten Elektronen (Hofstadter-Experimente)
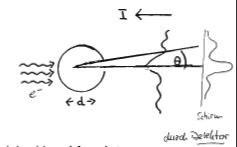
Beugungsmaxima und -minima
Für Kern , als 'Licht' sind hochbeschleunigte Elektronen gut geeignet (keine Starke WW).
Verknüpfung von Energie E, Impuls p und Wellenlänge durch relativistische Energiegleichung:
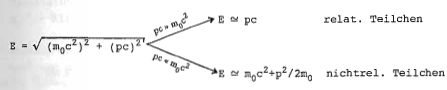
Für relat. Teilchen (, exakt für Teilchen mit Ruhemasse , d.h. Photonen, Neutrinos (?), Gravitonen (?), ... ) gilt wegen für die de Broglie-Wellenlänge :
Hofstädter-Experimente am Linearbeschleuniger in Stanford 1957 [1]
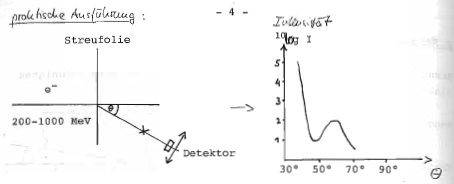
Ergebnis der Messungen für viele Elemente:
Genauer: kein scharfer Rand
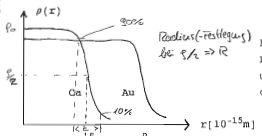
Quantitativ beschreibbar durch die Wood-Saxon-Formel:
Randbreite (90% 10% Abfall) 'Radius' m
Andere Meßmethoden zur Kernradienbestimmung: Isotopieverschiebung (Volumeneffekt) im optischen Bereich
Weitere Informationen
(gehört nicht zum Skript)
merken
- Kernradius , mit
- Masse
- Dichte ~
- Randschärfe
- Messung von Kernradien
- Erweiterung Mott Streuung mit Coulomb-Streuung von Elektronen (Spin an spinlosem Target))
3 Experimentelle Arten zur Bestimmung des Kernradius
- Hofstädter Experiment
mit [2]
- Wood Saxon Formel
- Geschwindigkeit >200 MeV mit De-Brogli Wellenlänge im fm Bereich
- Myonische Atome
- Isotopieverschiebung
Prüfungsfragen
- Äußere Eigenschaften eines Kerns
- Masse
- Randschärfe (vgl. Mit Atomhülle)
- Rutherfordscher Steuversuch
- Wie misst man Radius -> Streuexperimente (Rutherford erklärt)
- Was ist der differentielle Wirkungsquerschnitt?
- Was ist das für eine Größe? ->statistisch Abschätzung des Kernradius über kritischen Winkel, bei dem Abweichung vom Rutherfordstreuquerschnitt vorliegt.
- Was für eine Streuung liegt vor?-> elastische Streuung
- Was verändert sich bei inelastischer Streuung?->Energieübertrag an Target.
- Warum Goldfolie und kein Gas?
- Hofstädter Experiment
- Was ändert sich bei Hofstädter Experiment? -> Wellenmechanische Beschreibung des Streuproblems.
- Was wird gemessen?-> Ladungsverteilung.
- Wie sehen Ladungsverteilungen (Protonverteilung) aus?
- Wie sieht Neutronverteilung aus?-> Wood-Saxon Form aufmalen. Bei Protonen mit Anstieg beim Rand des Kerns.
- Was ergibt sich für den Wirkungsquerschnitt für ein Bild-> Bild mit Beugungsminima
- Warum?-> Analogie zur Beugung am Hindernis/Beugung am Einzelspalt.
- Welche Energie haben die Elektronen?-> 200MeV
- Warum?-> Damit Wellenlänge im fm-Bereich ist.
- Wie berechnet man die Wellenlänge? -> de Brouglie: lambda=hquer / omega
- Was für ein Beugungsbild bekommt man?-> Fraunhoferbeugung (Bild aufgemalt)
- Wie bekommt man aus Streuwirkungsquerschnitt die Ladungsverteilung? ->Streuwirkungsquerschnitt=Rutherfordquerschnitt mal Formfaktor (Fouriertrafo der Ladungsverteilung)
- Warum Formfaktor?
- -> bei Rutherford wurde von Punktladung ausgegangen, hier ausgedehnte Ladungsverteilung.
- -> Vorgehen Potential (Wood-Saxon-Form) raten und anpassen bis ermittelter Streuquerschnitt über Fouriertrafo der Ladungsverteilung und Rutherfordquerschnitt mit den Messwerten übereinstimmt.
- Warum Formfaktor?
- Warum keine „Vorwärtsrechnung“ möglich? (Vergleich mit Atomphysik) -> Hier komplizierter, da kein Zentralpotential und Überlagerung verschiedener Kräfte (Coulomb, starke, schwache WW).
- Kemradienmessung
- Rutherford -> Hofstädter (Formfaktor nur mit Leptonenstreuung, Mottstreuung erwähnt)
- Myonisches Atom (nur erwähnt)
- Wie misst man die Neutronenverteilung. daja vorherige Beispiele nur die Ladungsverteilung liefern? -> Streuung mit Hadronen wegen schwerer WW (z.B. a-Teilchen)

Literatur
- ↑ (Zusammenfassend: Rev. Mod. Phys. 1Q, 142-584 (1958) http://rmp.aps.org/abstract/RMP/v30/i2/p412_1)
- ↑ Bergmann-Schaefer: Lehrbuch der Experimentalphysik, Band 4: Bestandteile der Materie. 2. Auflage 2003, ISBN 978-3-11-016800-6 Gleichung 4.15