Bindungsenergien: Unterschied zwischen den Versionen
| (Eine dazwischenliegende Version desselben Benutzers wird nicht angezeigt) | |||
| Zeile 26: | Zeile 26: | ||
Prinzipieller Aufbau eines Energie und {{FB|Impulsfilter}}s in einem Massenspektrographen durch elektrische bzw. magnetische Felder: | Prinzipieller Aufbau eines Energie und {{FB|Impulsfilter}}s in einem [[Experiment::Massenspektrographen]] durch elektrische bzw. magnetische Felder: | ||
[[Datei:Energie_Impuls_Filter10.png|miniatur|zentriert|hochkant=3|Massenspektrographen Energie und Impulsfilter]] | [[Datei:Energie_Impuls_Filter10.png|miniatur|zentriert|hochkant=3|Massenspektrographen Energie und Impulsfilter]] | ||
| Zeile 45: | Zeile 45: | ||
;Helium: <math>d + d \to \alpha + 24 MeV, B(\alpha) = 28 MeV, B/A = 7 MeV</math> | ;Helium: <math>d + d \to \alpha + 24 MeV, B(\alpha) = 28 MeV, B/A = 7 MeV</math> | ||
== | ==Ergänzende Informationen== | ||
(gehört nicht zum Skript) | (gehört nicht zum Skript) | ||
[[Tröpfchenmodell,_Weizsäckersche_Massenformel|nächstes Kapitel]] | [[Tröpfchenmodell,_Weizsäckersche_Massenformel|nächstes Kapitel]] | ||
[[File:Auftragung Bindungsenergie gegen Massenzahl.svg|thumb|Auftragung Bindungsenergie gegen Massenzahl]] | [[File:Auftragung Bindungsenergie gegen Massenzahl.svg|thumb|Auftragung Bindungsenergie gegen Massenzahl]] | ||
Aktuelle Version vom 27. August 2011, 13:11 Uhr

|
Der Artikel Bindungsenergien basiert auf der Vorlesungsmitschrift von Moritz Schubotz des 3.Kapitels (Abschnitt 0) der Kern- und Strahlungsphysikvorlesung von Prof. Dr. P. Zimmermann. |
|}}
Die Abfrage enthält eine leere Bedingung.
Bindungsenergie
Da man die Massenbestimmung mit atomphysikalischen Meßmethoden
(Massenspektrometer) durchführt, versteht man unter Mc² die Masse
des Atoms, d.h. man muß noch die Elektronenmassen abzüglich ihrer
Bindungsenergien berücksichtigen. Deshalb bezieht man die
Masseneinheit 1 auf 1/12 der Masse des neutralen -Atoms.
| ANMERKUNG Schubotz: Oftmals wird die Wasserstoffmasse statt der Protonenmasse zur Berechnung der Binduungsenergie verwendet, da so die Elektronenmassen implizit berücksichtigt werden. |
Massenspektrometrie
Prinzip der Massenspektrometrie: Durch die Messung der Energie und des Impulses wird die Masse bestimmt.
Prinzipieller Aufbau eines Energie und Impulsfilters in einem Massenspektrographen durch elektrische bzw. magnetische Felder:
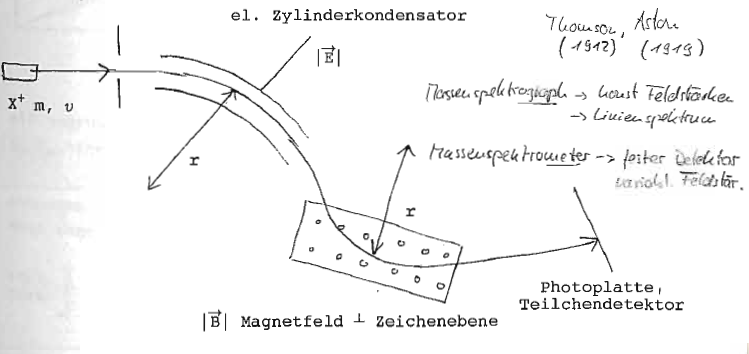
- el. Feld
- ·Energiemessung
- magn. Feld
- Impulsmessung
Bindungsenergie pro Nukleon
Ergebnis für Bindungsenergie pro Nukleon B/A

Im Mittel , d.h. ~ 1% der Ruhemasse •
Maximum bei ca. (Eisen), danach wegen wachsender Coulombabstoßung Abnahme um ca. 1 MeV auf bei . Größere Unregelmäßigkeiten bei leichten Kernen bis , besonders ausgeprägt bei:
Ergänzende Informationen
(gehört nicht zum Skript)

merken
Idee: Zentripetalkraft = Lorentzkraft
merke Spektrograph erzeugt Bild
Auflösungsvermögen absoulute Massenbestimmung (bekannte Radien, E und B Felder, Ladung (5-Größen))
Ladung muss bekannt sein und ungleich 0 sein --> Neutronenmasse nicht bestimmbar (Umweg Deuteriumkern, Bindungsenergie)
Prüngsfragen
- Massenspektrometer (hier etwas genauer, mit Skizze und Funktionsweise.
- Was ist der Hauptanteil der relativ kleinen Fehler? -> inhomogenitäten an den Rändern der Felder)
Häufigkeit:2
Quellen
- ↑ Bergmann-Schaefer: Lehrbuch der Experimentalphysik, Band 4: Bestandteile der Materie. 2. Auflage 2003, ISBN 978-3-11-016800-6 Gl. 4.7