Kerndrehimpulse und elektromagnetische Kernmomente: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
|||
| (11 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
Der {{FB|Kerndrehimpuls}} I setzt sich aus den {{FB|Bahndrehimpuls}}en <math> | Der {{FB|Kerndrehimpuls}} I setzt sich aus den {{FB|Bahndrehimpuls}}en <math>l_i</math> und | ||
{{FB|Spin}}s <math>s_i</math> der elnzelnen Nukleonen zusammen. | |||
<math> | : <math>\vec I = \sum \vec l_i + \vec s_i</math>. | ||
Bahndrehimpulse | |||
<math>l_i</math> als Erhaltungsgrößen setzen ein Zentralpotential <math>V = V(r)</math> voraus, in dem sich die Nukleonen praktisch frei und ohne | |||
Stöße im Kerninneren bewegen. Diese Einteilchenvorstellung, welche die Basis des Schalenmodells (Kap. 7) ist, hat ihre Begründung darin, | Stöße im Kerninneren bewegen. Diese Einteilchenvorstellung, welche die Basis des Schalenmodells (Kap. 7) ist, hat ihre Begründung darin, | ||
daß die Nukleonen als Fermionen im Grundzustand alle nach dem Pauli-Prinzip erlaubten Zustände besetzen, so daß es keine "Stöße" | daß die Nukleonen als {{FB|Fermionen im Grundzustand}} alle nach dem {{FB|Pauli-Prinzip}} erlaubten Zustände besetzen, so daß es keine "Stöße" | ||
gibt und die Nukleonen quasi als freie Teilchen auftreten. | gibt und die Nukleonen quasi als freie Teilchen auftreten. | ||
| Zeile 14: | Zeile 17: | ||
[[Datei:Drehimpuls-z16.png|miniatur|'Vektor'-Modell]] | [[Datei:Drehimpuls-z16.png|miniatur|'Vektor'-Modell]] | ||
Operatorenzuordnung <math>p \to \frac{\hbar}{i} \nabla</math>, Separation der Wellenfunktionen <math>\psi_{nlm}(r)=R_{nl}(r)Y_{lm}(\theta,\phi)</math> | Operatorenzuordnung <math>p \to \frac{\hbar}{i} \nabla</math>, Separation der Wellenfunktionen <math>\psi_{nlm}(r)=R_{nl}(r)Y_{lm}(\theta,\phi)</math> | ||
in Radial- und Winkelteil. Die sphärischen Kugelfunktionen <math>Y_{lm}(\theta,\phi)</math> sind die Eigenfunktionen von <math>l^2</math> und <math>l_z</math> mit den Eigenwerten <math> | in Radial- und Winkelteil. Die sphärischen Kugelfunktionen <math>Y_{lm}(\theta,\phi)</math> sind die Eigenfunktionen von <math>l^2</math> und <math>l_z</math> mit den Eigenwerten <math>l(l+1)\hbar^2</math> und <math>m\hbar</math>. | ||
l = 0, 1, 2, 3, 4, ... | |||
s, p, d, f, g spektr. Bezeichnung | s, p, d, f, g spektr. Bezeichnung | ||
<math>l^2 Y_{lm}(\theta,\phi) = ( | <math>l^2 Y_{lm}(\theta,\phi) = (l+1)\hbar^2 Y_{lm}(\theta,\phi)</math> | ||
m = -l, ... 0, ... +l | m = -l, ... 0, ... +l | ||
<math>\to 2l+1</math> Einstellmöglichkeiten | :<math>\to 2l+1</math> Einstellmöglichkeiten | ||
| Zeile 29: | Zeile 32: | ||
==Spin== | ==Spin== | ||
[[Datei:Spin-17.png|miniatur|Spin-Darstellung]] | [[Datei:Spin-17.png|miniatur|Spin-Darstellung]] | ||
Spin <math>s ,s =\dfrac{1}{2}</math> | Spin <math>\vec s ,s =\dfrac{1}{2}</math> | ||
Ergebnis der relat. Quantenmechanik ({{FB|Diractheorie}}). Halbzahlige Spin-Teilchen (z.B. n, p, e, ... ) sind Fermionen, deren Wellenfunktionen bei Teilchentausch sich anti symmetrisch verhalten ({{FB|Pauli-Prinzip}}). | Ergebnis der relat. Quantenmechanik ({{FB|Diractheorie}}). '''Halbzahlige''' Spin-Teilchen (z.B. n, p, e, ... ) sind Fermionen, deren Wellenfunktionen bei Teilchentausch sich anti symmetrisch verhalten ({{FB|Pauli-Prinzip}}). | ||
Im Gegensatz dazu sind ganzteilige Spin-Teilchen (einschließlich s = 0) Bosonen, | Im Gegensatz dazu sind '''ganzteilige''' Spin-Teilchen (einschließlich s = 0) Bosonen, | ||
(z.B. d, <math>\alpha</math>, Photonen, Pionen) mit bei Teilchentausch symmetrischen | (z.B. d, <math>\alpha</math>, Photonen, Pionen) mit bei Teilchentausch symmetrischen | ||
Wellenfunktionen. Unterschiedliche Statistik. | Wellenfunktionen. Unterschiedliche Statistik. | ||
| Zeile 44: | Zeile 47: | ||
Bei mehreren Nukleonen gibt es verschiedene Kopplungsmöglichkeiten, | Bei mehreren Nukleonen gibt es verschiedene Kopplungsmöglichkeiten, | ||
wie beispielsweise in der Atomphysik die {{FB|LS-Kopplung}} mit | wie beispielsweise in der Atomphysik die | ||
<math> \vec L = \sum \vec l_i, \quad \vec S= \sum \vec s_i, \quad \vec L+ \vec S= \vec I</math> oder die {{FB|jj-Kopplung}} mit | :{{FB|LS-Kopplung}} mit <math> \vec L = \sum \vec l_i, \quad \vec S= \sum \vec s_i, \quad \vec L+ \vec S= \vec I</math> oder die | ||
<math> \vec l_i+ \vec s_i= \vec j_i, \quad \sum \vec j = \vec I</math>. | :{{FB|jj-Kopplung}} mit <math> \vec l_i+ \vec s_i= \vec j_i, \quad \sum \vec j = \vec I</math>. | ||
| Zeile 58: | Zeile 60: | ||
Neigung der Protonen und Neutronen, sich jeweils paarweise durch "Antiparallelstellung" der Einzeldrehimpulse mit <math>\vec j_{p_i}+ \vec j_{p_k} = 0</math> bzw. <math> \vec j_{n_i}+ \vec j_{n_k} = 0</math> zu kompensieren. | Neigung der Protonen und Neutronen, sich jeweils paarweise durch "Antiparallelstellung" der Einzeldrehimpulse mit <math>\vec j_{p_i}+ \vec j_{p_k} = 0</math> bzw. <math> \vec j_{n_i}+ \vec j_{n_k} = 0</math> zu kompensieren. | ||
Folgerung für (u, g)- und (g, u)-Kerne | Folgerung für (u, g)- und (g, u)-Kerne | ||
<math> \vec I(u, g) = \vec I(g,g-\textrm{Rumpf}) + \vec j_P \to \vec I(u, g) = \vec j_p</math> | <math> \vec I(u, g) = \vec I(g,g-\textrm{Rumpf}) + \vec j_P \to \vec I(u, g) = \vec j_p</math> | ||
d. h. | d. h. I(u, g) = Einzeldrehimpuls <math> \vec j_p</math> des letzten ungepaarten Protons | ||
Entsprechend <math>1(g, u) = j_n</math> Einzeldrehimpuls des letzten ungepaarten | Entsprechend <math>1(g, u) = j_n</math> Einzeldrehimpuls des letzten ungepaarten | ||
Neutrons. | Neutrons. | ||
| Zeile 71: | Zeile 72: | ||
Mit dem Bahndrehimpuls und Spin der Nukleonen sind magnetische Dipolmomente verbunden. | Mit dem Bahndrehimpuls und Spin der Nukleonen sind magnetische Dipolmomente verbunden. | ||
=== Bahn === | === Bahn === | ||
[[Datei:BahnDrehmoment19.png]] | [[Datei:BahnDrehmoment19.png|framed|magnetisches Dipolmoment]] | ||
magn. Dipolmoment = <math>c^{-1}</math> Strome Fläche | |||
:<math>\mu_l=\frac{e\hbar}{2mc}\vec l=\frac{1}{c}\frac{e v}{2 \pi r} \pi r^2</math> mit <math>\hbar l = mrv</math> | |||
<math>\mu_l=\frac{e\hbar}{2mc}l=\frac{1}{c}\frac{e v}{2 \pi r} \pi r^2</math> | ;Bohrsches Magneton: <math>m=m_0</math> Elektron <math>\frac{e \hbar}{2m_0 c}=\mu_b=0,927\times 10^{-23} J/T</math> | ||
;Bohrsches Magneton: <math>m=m_0</math> Elektron <math>\frac{e \hbar}{2m_0 c}=\mu_b=0 | ;Kernmagneton:<math>m = m_p</math> Proton <math>\frac{e\hbar}{2m_p c} = \mu_K = 0,505\times10^{-26} J/T</math> | ||
;Kernmagneton:<math>m = m_p</math> Proton <math>\frac{e\hbar}{ | |||
=== Spin=== | === Spin=== | ||
Für <math>s = \tfrac{1}{2}</math>-Teilchen erwartet man in Analogie zum Bahnbeitrag | Für <math>s = \tfrac{1}{2}</math>-Teilchen erwartet man in Analogie zum Bahnbeitrag | ||
:<math>\mu_s=\frac{e\hbar}{2 m c} s , s=\dfrac{1}{2}</math> Falsch! | :<math>\mu_s=\frac{e\hbar}{2 m c} s , s=\dfrac{1}{2}</math> '''Falsch'''! | ||
Experimentell gilt allgemein | Experimentell gilt allgemein | ||
:<math>\mu_s=g \frac{e\hbar}{2 m c} s</math> g-Faktor | :<math>\mu_s=g \frac{e\hbar}{2 m c} s</math> {{FB|g-Faktor}} | ||
Dabei ist für das Elektron <math>g = -2</math> nach der Diractheorie bis auf | Dabei ist für das Elektron <math>g = -2</math> nach der Diractheorie bis auf | ||
kleinere quantenelektrodynamische Korrekturen bestätigt. Für Proton | kleinere quantenelektrodynamische Korrekturen bestätigt. Für Proton | ||
und Neutron erwartet man deshalb <math>g_p = 2</math> und <math>g_n = 0</math> (wegen fehlender | und Neutron erwartet man deshalb <math>g_p = 2</math> und <math>g_n = 0</math> (wegen fehlender Ladung). | ||
Ladung). Die gemessenen Werte <math>g_p = 5,586</math> und <math>g_n = -3,826</math> jedoch, daß die Nukleonen keine einfachen "Punkt-Teilchen" | Die gemessenen Werte | ||
sind. | :<math>g_p = 5,586</math> und | ||
:<math>g_n = -3,826</math> zeigen jedoch, daß die Nukleonen keine einfachen "Punkt-Teilchen" sind. | |||
Die magnetischen Kerndipolmomente <math>\mu_I</math> für (g, u)- und (u,g)-Kerne lassen sich (zumindest für leichte Kerne) näherungsweise auf den des letzten ungepaarten Nukleons zurückführen (Schmidt-Modell). | |||
{{AnMS|g-Faktor auch Lande Faktor gibt theoretisch für ein geladenes Teilchen im Magnetfeld an, um wie viel stärker sich der Spin auf seine Energie auswirkt als ein gleich großer Bahndrehimpuls}} | |||
==Elektrisches Kernquadrupolmoment Q== | ==Elektrisches Kernquadrupolmoment Q== | ||
| Zeile 100: | Zeile 101: | ||
Q gibt Abweichung von der Kugelgestalt wieder | Q gibt Abweichung von der Kugelgestalt wieder | ||
Potential \phi für p im Außenraum <math>\Delta \phi = 0</math> | Potential <math>\phi</math> für p im Außenraum <math>\Delta \phi = 0</math> | ||
:<math>\phi(r,\theta) = \frac{1}{4 \pi \epsilon_0} \sum\limits_{n=0}^{\infty} a_n \frac{1}{r^{n+1}} P_n(\cos \theta)</math> | :<math>\phi(r,\theta) = \frac{1}{4 \pi \epsilon_0} \sum\limits_{n=0}^{\infty} a_n \frac{1}{r^{n+1}} P_n(\cos \theta)</math> | ||
| Zeile 106: | Zeile 107: | ||
:<math>P_1 = cos \theta \quad P_n(\theta = 0) = 1 \quad P_2 = \frac{1}{2} + \frac{3}{2} \cos^ 2 \theta</math> | :<math>P_1 = cos \theta \quad P_n(\theta = 0) = 1 \quad P_2 = \frac{1}{2} + \frac{3}{2} \cos^ 2 \theta</math> | ||
[[Datei:KernQuadrupolmoment20.png|miniatur]] | [[Datei:KernQuadrupolmoment20.png|miniatur|Kugelgestalt des Kerns]] | ||
Die Bedeutung der Entwicklungskoeffizienten <math>a_n</math> erkennt man durch direkte Berechnung des Potentials auf der z-Achse, also für <math>e = 0</math> und Koeffizientenvergleich: | Die Bedeutung der Entwicklungskoeffizienten <math>a_n</math> erkennt man durch direkte Berechnung des Potentials auf der z-Achse, also für <math>e = 0</math> und Koeffizientenvergleich: | ||
:<math>\phi(r,\theta=0) = \frac{1}{4 \pi \epsilon_0} \sum\limits_{n=0}^{\infty} a_n \frac{1}{r^{n+1}} 1</math> | :<math>\phi(r,\theta=0) = \frac{1}{4 \pi \epsilon_0} \sum\limits_{n=0}^{\infty} a_n \frac{1}{r^{n+1}} 1</math> | ||
| Zeile 122: | Zeile 123: | ||
Größenordnung: <math>Q \approx \pi R^2 \approx 10^{-28} m^2</math> (lb) | Größenordnung: <math>Q \approx \pi R^2 \approx 10^{-28} m^2</math> (lb) | ||
Vorzeichen: | Vorzeichen: | ||
[[Datei:KernQuadrupolmoment-Geometry21.png]] | [[Datei:KernQuadrupolmoment-Geometry21.png|gerahmt|Formen des Kernquadupolmoments]] | ||
==Ergänzende Infromationen== | |||
(gehört nicht zum Skript) | |||
===Prüfungsfragen=== | |||
* Äußere Eigenschaften eines Kerns | |||
** magnetische Momente (phänomenolog.), cl. Ladung und Multipolmomente -> empirische Befunde -> Modell inkopressibler Kernmaterie | |||
*Kerndrehimpulse und elektromagnetische Kernmomente | |||
**Drehimpulse + magnet. Momente von Kernen; was ist das + wie misst man das Modellvorstellung gg ,gu/ug, uu Experiment: Rabi Anwendung -> MRT | |||
Aktuelle Version vom 28. August 2011, 14:22 Uhr

|
Der Artikel Kerndrehimpulse und elektromagnetische Kernmomente basiert auf der Vorlesungsmitschrift von Moritz Schubotz des 5.Kapitels (Abschnitt 0) der Kern- und Strahlungsphysikvorlesung von Prof. Dr. P. Zimmermann. |
|}}
Die Abfrage enthält eine leere Bedingung.
Der Kerndrehimpuls I setzt sich aus den Bahndrehimpulsen und
Spins der elnzelnen Nukleonen zusammen.
Bahndrehimpulse als Erhaltungsgrößen setzen ein Zentralpotential voraus, in dem sich die Nukleonen praktisch frei und ohne Stöße im Kerninneren bewegen. Diese Einteilchenvorstellung, welche die Basis des Schalenmodells (Kap. 7) ist, hat ihre Begründung darin, daß die Nukleonen als Fermionen im Grundzustand alle nach dem Pauli-Prinzip erlaubten Zustände besetzen, so daß es keine "Stöße" gibt und die Nukleonen quasi als freie Teilchen auftreten.
Bahndrehimpuls
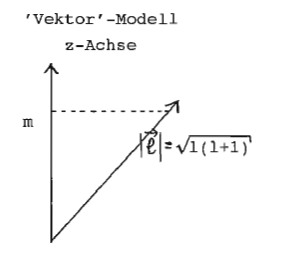
Operatorenzuordnung , Separation der Wellenfunktionen in Radial- und Winkelteil. Die sphärischen Kugelfunktionen sind die Eigenfunktionen von und mit den Eigenwerten und .
l = 0, 1, 2, 3, 4, ...
s, p, d, f, g spektr. Bezeichnung
m = -l, ... 0, ... +l
Spin
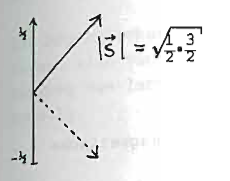
Ergebnis der relat. Quantenmechanik (Diractheorie). Halbzahlige Spin-Teilchen (z.B. n, p, e, ... ) sind Fermionen, deren Wellenfunktionen bei Teilchentausch sich anti symmetrisch verhalten (Pauli-Prinzip). Im Gegensatz dazu sind ganzteilige Spin-Teilchen (einschließlich s = 0) Bosonen, (z.B. d, , Photonen, Pionen) mit bei Teilchentausch symmetrischen Wellenfunktionen. Unterschiedliche Statistik.
Gesamtdrehimpuls
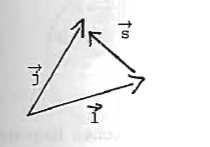
Gesamtdrehimpuls eines einzelnen Nukleons ~ "parallel" oder"antiparallel"
Bei mehreren Nukleonen gibt es verschiedene Kopplungsmöglichkeiten,
wie beispielsweise in der Atomphysik die
- LS-Kopplung mit oder die
- jj-Kopplung mit .
Experimentelle Ergebnisse für die Kerndrehimpulse I:
(g, g) I = 0 (im Grundzustand)
(u, g) , (g, u) I = 1/2, 3/2, 5/2, ...
(u, u) = 0, 1, 2, 3, ...
Neigung der Protonen und Neutronen, sich jeweils paarweise durch "Antiparallelstellung" der Einzeldrehimpulse mit bzw. zu kompensieren.
Folgerung für (u, g)- und (g, u)-Kerne
d. h. I(u, g) = Einzeldrehimpuls des letzten ungepaarten Protons Entsprechend Einzeldrehimpuls des letzten ungepaarten Neutrons.
Magnetisches Kerndipolmoment µI
Mit dem Bahndrehimpuls und Spin der Nukleonen sind magnetische Dipolmomente verbunden.
Bahn
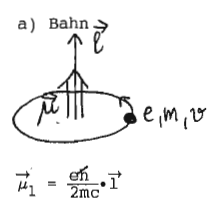
magn. Dipolmoment = Strome Fläche
Spin
Für -Teilchen erwartet man in Analogie zum Bahnbeitrag
Experimentell gilt allgemein
Dabei ist für das Elektron nach der Diractheorie bis auf kleinere quantenelektrodynamische Korrekturen bestätigt. Für Proton und Neutron erwartet man deshalb und (wegen fehlender Ladung). Die gemessenen Werte
Die magnetischen Kerndipolmomente für (g, u)- und (u,g)-Kerne lassen sich (zumindest für leichte Kerne) näherungsweise auf den des letzten ungepaarten Nukleons zurückführen (Schmidt-Modell).
| ANMERKUNG Schubotz: g-Faktor auch Lande Faktor gibt theoretisch für ein geladenes Teilchen im Magnetfeld an, um wie viel stärker sich der Spin auf seine Energie auswirkt als ein gleich großer Bahndrehimpuls |
Elektrisches Kernquadrupolmoment Q
Q gibt Abweichung von der Kugelgestalt wieder
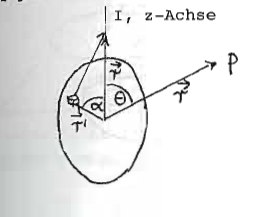
Die Bedeutung der Entwicklungskoeffizienten erkennt man durch direkte Berechnung des Potentials auf der z-Achse, also für und Koeffizientenvergleich:
oder direkt berechnet
- n=0
- Punktladung
- n=1
- elektrisches Dipolmoment in -Richtung (=0 da Kernkräfte die Parität erhalten)
- n=2
Bei konstanter Ladungsverteilung ist deshalb .
Größenordnung: (lb)
Vorzeichen:
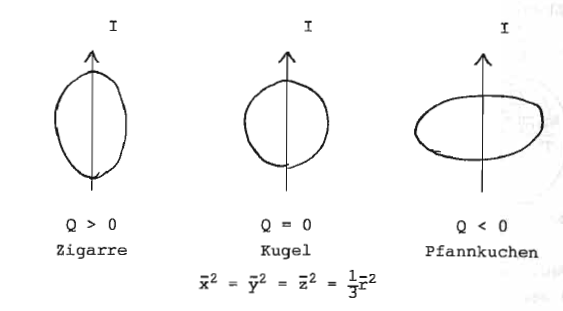
Ergänzende Infromationen
(gehört nicht zum Skript)
Prüfungsfragen
- Äußere Eigenschaften eines Kerns
- magnetische Momente (phänomenolog.), cl. Ladung und Multipolmomente -> empirische Befunde -> Modell inkopressibler Kernmaterie
- Kerndrehimpulse und elektromagnetische Kernmomente
- Drehimpulse + magnet. Momente von Kernen; was ist das + wie misst man das Modellvorstellung gg ,gu/ug, uu Experiment: Rabi Anwendung -> MRT