Alpha-Zerfall: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
|||
| (2 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 27: | Zeile 27: | ||
Für "dicke" Barriere Kd >> 1 ist e<sup>Kd</sup> der beherrschende Faktor, d.h. | Für "dicke" Barriere Kd >> 1 ist e<sup>Kd</sup> der beherrschende Faktor, d.h. | ||
<math>T \approx e^{- 2Kd}</math>. Für allgemeinen Potentialverlauf: <math>T \approx e^{- 2G}</math> mit {{FB|Gamowfaktor}} <math>G =\int Kdr</math>, z. B. für {{FB|Coulombpotential}} ist der Gamowfaktor in mathematisch geschlossener Form angebbar und tabelliert. | <math>T \approx e^{- 2Kd}</math>. Für allgemeinen Potentialverlauf: <math>T \approx e^{- 2G}</math> mit {{FB|Gamowfaktor}} <math>G =\int Kdr</math>, z. B. für {{FB|Coulombpotential}} ist der Gamowfaktor in mathematisch geschlossener Form angebbar und tabelliert. | ||
{{AnMS|Vorgerechnet in {{Quelle|VLKP|??}} <math>G=\sqrt{\frac{2m}{\hbar Q}}\frac{Z Z' e^2}{4 \pi \epsilon_0}\underbrace{\left[\arccos\sqrt\frac{Q}B- \sqrt{\frac{Q}{B}(1-\frac{Q}{B})}\right]}_{Q \ll B \to \sim \frac\pi2}</math>}} | |||
| Zeile 52: | Zeile 54: | ||
===Prüfungsfragen=== | ===Prüfungsfragen=== | ||
Frage zum <math>\alpha</math>-Zerfall (Gamow-Faktor mit Abhängikeiten). (Prof. Kanngießer) | Frage zum <math>\alpha</math>-Zerfall (Gamow-Faktor mit Abhängikeiten). (Prof. Kanngießer) | ||
<references /> | |||
Aktuelle Version vom 28. August 2011, 15:05 Uhr

|
Der Artikel Alpha-Zerfall basiert auf der Vorlesungsmitschrift von Moritz Schubotz des 11.Kapitels (Abschnitt 0) der Kern- und Strahlungsphysikvorlesung von Prof. Dr. P. Zimmermann. |
|}}
Die Abfrage enthält eine leere Bedingung.
- Warum nicht p, n, d-, sondern α-Zerfall?
- Grund
- Die hohe Bindungsenergie Eα = 28 MeV bewirkt, daß diese Energie besonders für schwere Kerne (ab ca. 200U) oft größer ist als die Ablösearbeit von 2 Protonen und 2 Neutronen,
so daß -Zerfall energetisch möglich wird.
- Warum nicht spontaner Zerfall in für Kernreaktionen typischen Zeiten von 10-21 s?
- Grund
- Coulombbarriere, Tunneleffekt
Tunneleffekt (Gamow): "Überspringen der Barriere wegen Energieunschärferelation
". Vereinfacht mit Rechteckbarriere:
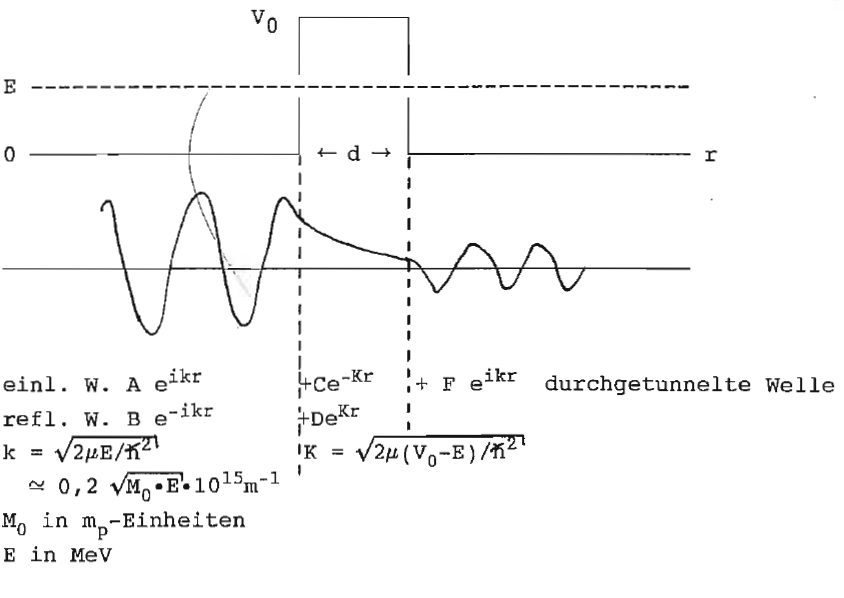
Anpassung der Wellenfunktionen und ihrer Ableitungen an den beiden Sprungstellen ergibt 4 Bestimmungsgleichungen für die 5 Amplituden A, B, C, D, F (A Normierung).
Für "dicke" Barriere Kd >> 1 ist eKd der beherrschende Faktor, d.h. . Für allgemeinen Potentialverlauf: mit Gamowfaktor , z. B. für Coulombpotential ist der Gamowfaktor in mathematisch geschlossener Form angebbar und tabelliert.
| ANMERKUNG Schubotz: Vorgerechnet in [1] |
Somit Übergangswahrscheinlichkeit A für α-Zerfall:

Weitere Informationen
(gehört nicht zum Skript)
- siehe lok. Maximum bei He in Darstellung der Bethe-Weizäcker Formel für E_B/A
- Extraktion eines Schweren Kerns unwahrscheinlicher als durch Gamow-Faktor auszurechnen da sich mehr Nukleonen im Kerninneren zu einem gebilde mit passendem (N,Z) formieren müssen
- Q-Wert Höhe des präformierten Teilches über dem Grudniveau des Potetntialtopfes
Prüfungsfragen
Frage zum -Zerfall (Gamow-Faktor mit Abhängikeiten). (Prof. Kanngießer)
- ↑ VLKP,??
