Synchrotron- und Laserstrahlung: Unterschied zwischen den Versionen
Die Seite wurde neu angelegt: „<noinclude>{{ScriptProf|Kapitel=17|Abschnitt=0|Prof=Prof. Dr. P. Zimmermann|Thema=Kern- und Strahlungsphysik|Schreiber=Moritz Schubotz}}</noinclude>“ |
|||
| (13 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
<noinclude>{{ScriptProf|Kapitel=17|Abschnitt=0|Prof=Prof. Dr. P. Zimmermann|Thema=Kern- und Strahlungsphysik|Schreiber=Moritz Schubotz}}</noinclude> | <noinclude>{{ScriptProf|Kapitel=17|Abschnitt=0|Prof=Prof. Dr. P. Zimmermann|Thema=Kern- und Strahlungsphysik|Schreiber=Moritz Schubotz}}</noinclude> | ||
Wichtigste experimentelle Entwicklungen der letzten 20 Jahre: | |||
Speicherringe (Hochenergiephysik) und Laser. | |||
== Synchrotronstrahlung == | |||
[[Datei:17.1.synchrotronstrahlung.png|miniatur|hochkant=3|zentriert|Maxwell-GI., retardierte Potentiale | |||
(Relat.theorie) - Schwinger-Gleichungen]] | |||
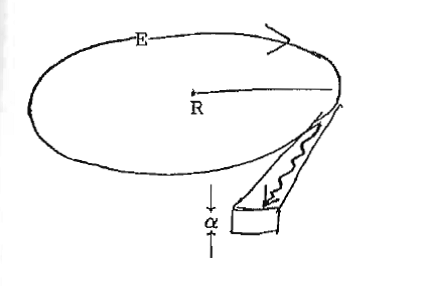
[[Datei:17.2.synchrotronstrahlung.bessy.png|miniatur|hochkant=3|zentriert|z.B. 800 MeV, R ~ 1,8 m (BESSY)]] | |||
===Spektralverteilung der Strahlung=== | |||
:<math>I(\lambda)\sim(\frac{\lambda_c}{\lambda})^4,\quad \lambda \gtrsim \lambda_c</math> | |||
kritische Wellenlänge | |||
<math>{{\lambda }_{c}}=\frac{4\pi R}{3{{\gamma }^{3}}},\quad \gamma =\frac{E}{m{{c}^{2}}}</math> | |||
BESSY: <math>R ~ 1,8 m, E \approx 800 MeV \to \gamma \approx 1600 : \lambda_c\approx 2 nm</math> | |||
===Vertikale Divergenz <math>\alpha</math>:=== | |||
<math>\alpha =\frac{2}{3\gamma }{{\left( \frac{\lambda }{{{\lambda }_{C}}} \right)}^{1/3}}\quad \lambda \gtrsim {{\lambda }_{C}}</math> | |||
z.B. | |||
<math>\lambda =100\text{nm}\to \alpha \approx 1,5\text{mrad}</math> | |||
===Zeitstruktur:=== | |||
Im Multi-bunch-Betrieb ca. 100 bunches (1 ~ 3 cm) im Ring von | |||
l = 60 m und 500 MHz HF-Sender: | |||
100 ps-Pulse mit 2 ns-Abstand (Umlaufzeit 200 ns) | |||
== Laser == | |||
===Grundgleichungen=== | |||
Lasertypen: | |||
*Gaslaser: He-Ne, Edelgasionen-Laser (CW), N<sub>2</sub>-, Excimer-Laser (gepulst) | |||
*Festkörper: Nd:YAG-, Rubin-, Halbleiter-Laser | |||
*Flüssigkeit: Farbstofflaser | |||
Bestimmende Größen: | |||
*{{FB|Wellenlänge}}: <math>\lambda</math>, | |||
*{{FB|Schärfe}}: <math>d\lambda</math>, | |||
*{{FB|Abstimmbereich}}: <math>\Delta \lambda</math>, | |||
*{{FB|Divergenz}}: <math>d\Omega</math>, | |||
*{{FB|Leistung}}: L | |||
Bei Pulsbetrieb: | |||
*{{FB|Pulsbreite}}: <math>\Delta t</math>, | |||
*{{FB|Pulsenergie}}: E, | |||
*{{FB|Repetitionsrate}} | |||
Grundgleichungen: | |||
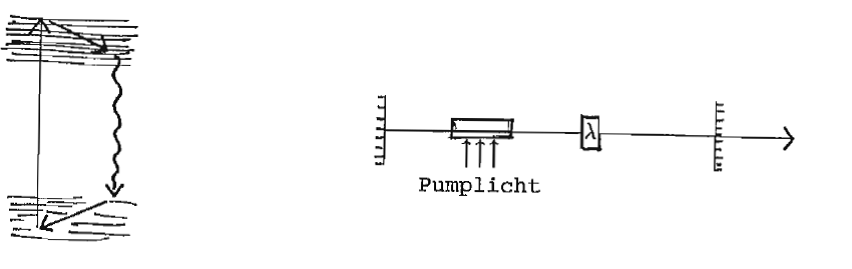
[[Datei:17.3.laser.schema.png|miniatur|zentriert|hochkant=3]] | |||
Im thermodynamischen Gleichgewicht: | |||
:<math>A_{21}N_2 + B_{21} \rho(\gamma) N_2 = B_{12} \rho(\gamma)N_1</math> | |||
mit Boltzmann <math>N_2/N_1 = g_2/g_1 \exp(- h\nu/kT)</math> verwenden, nach <math>\rho(\nu)</math> auflösen | |||
und mit {{FB|Planckschem Strahlungsgesetz}} vergleichen, ergibt | |||
a) <math>g_1 B_{12} = g_2 B_{21}</math> --> Besetzungsinversion notwendig | |||
b) <math>A_{21}=B_{21} \frac{8\pi}{c^3}h\nu^3</math> -> <math>\nu^3</math>-Zunahme der störenden Spontanemission (siehe Röntgenlaserentwicklung) | |||
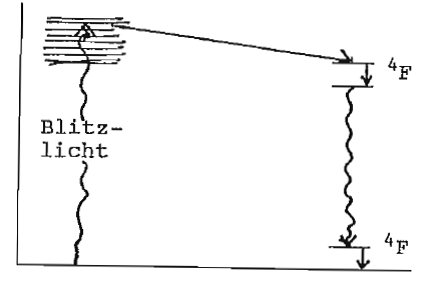
[[Datei:17.4.niveau.laser.png|miniatur|zentriert|hochkant=3|Pumpschema 4-Niveau Laser]] | |||
===Einige Lasertypen=== | |||
[[Datei:17.5.edelgasionenlaser.png|miniatur|zentriert|hochkant=3|{{FB|Edelgasionenlaser}} z. B. Ar<sup>+</sup>- Laser]] | |||
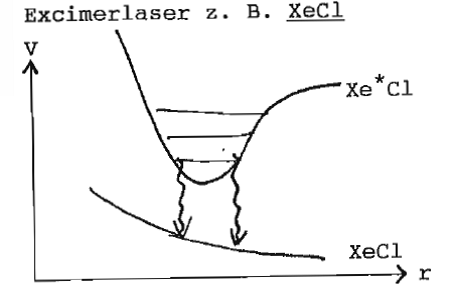
[[Datei:17.6.excimerlaser.png|miniatur|zentriert|hochkant=3|{{FB|Excimerlaser}} z. B. XeCl | |||
gepulst, UV 351 - 353 nm | |||
1 - 2 bar He Puffergas, 1 - 10% Xe, | |||
0,2 % HCl, Pulslängen 5 - 15 ns, | |||
Repetitionsrate ~ 100 Hz - 1 kHz | |||
Impulsenergie ~ J Puls-Leistung | |||
1J/10 ns = 100 MW | |||
(Dauerleistung ~ 1 - 100 W)]] | |||
[[Datei:17.7.NdYAG-Laser.png|miniatur|zentriert|hochkant=3|{{FB|Nd:YAG-Laser}} Yttriumaluminiumgranulat <math>Y_2Al_5O_{12}</math> +0,7% Nd: <math>Nd^{3+} 4d^{10} 4f^{3} 5s^2 5p^6</math> | |||
4f-Schale durch ss, sp abgeschirmt, | |||
Kristallfeldenfluß | |||
deshalb relativ gering | |||
]] | |||
[[Datei:17.8.Farbstofflaser.png|miniatur|zentriert|hochkant=3|Farbstofflaser]] | |||
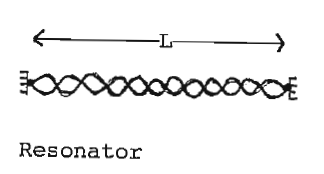
[[Datei:17.9.einmodenlaser.png|miniatur|zentriert|hochkant=3|Einmodenlaser]] | |||
Resonator <math>L=m\frac{\lambda }{2}</math>, | |||
<math>\lambda =\frac{2L}{m},\nu =\frac{c}{\lambda }=\frac{cm}{2L}</math> | |||
(longitudinaler) Modenabstand | |||
<math>d\lambda =\frac{2L}{{{m}^{2}}},d\nu =\frac{c}{2L}\left( =\frac{c}{{{\lambda }^{2}}}d\lambda \right)</math> | |||
z.B. | |||
<math>L=1\text{m}\to d\nu =\frac{3\cdot {{10}^{8}}\text{m/s}}{2\text{m}}=150\text{MHz}</math> | |||
z.B. | |||
<math>\lambda =500\text{nm}\quad d\lambda =\frac{{{\lambda }^{2}}}{c}d\nu =\frac{25\cdot {{10}^{-14}}{{\text{m}}^{\text{2}}}}{3\cdot {{10}^{8}}\text{m/s}}1,5\cdot {{10}^{8}}\text{/s}=1,25\cdot {{10}^{-13}}\text{m}=0,125\text{pm}=1,25\cdot {{10}^{-3}} \AA</math> | |||
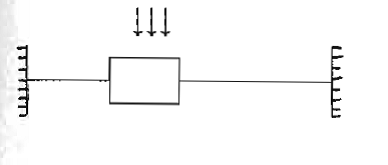
[[Datei:17.10.pumplicht.png|miniatur|zentriert|hochkant=3]] | |||
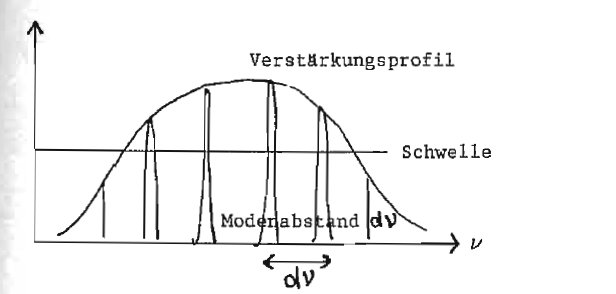
[[Datei:17.11.verstaerkungsprofil.png|miniatur|zentriert|hochkant=3]] | |||
Verstärkerprofil z. B. Dopplerbreite, Druckverbreiterung, Stöße | |||
Dopplerbreite | |||
<math>\frac{\Delta {{\nu }_{D}}}{\nu }=\frac{\Delta {{\lambda }_{D}}}{\lambda }=\frac{v}{c},\quad \frac{v}{c}=\frac{\sqrt{3kT}}{m{{c}^{2}}}\approx {{10}^{-6}}</math> | |||
[[Datei:17.12.verbreiterung.png]] | |||
z. B. | |||
<math>\lambda =500\text{nm}</math> | |||
bzw. | |||
<math>\nu =c/\lambda =\frac{3\cdot {{10}^{8}}}{5\cdot {{10}^{-7}}}\text{Hz}=6\cdot {{10}^{14}}\text{Hz}</math> | |||
:<math>\begin{align} | |||
& \Delta {{\lambda }_{D}}=0,5\text{pm} \\ | |||
& \Delta {{\nu }_{D}}=600\text{MHz} \\ | |||
\end{align}</math> | |||
Exp. Beispiele: | |||
*HeNe <math>\Delta {{\nu }_{D}}=1500 MHz</math> | |||
*Ar+ <math>\Delta {{\nu }_{D}}=8000 MHz</math> | |||
*Farbstoff <math>\Delta {{\nu }_{D}}= 103 GHz</math> (starke Stoßverbreiterung) | |||
Einmodenlaser: Stufenweise Einschränkung durch verschiedene optische | |||
Filter (Lyot, {{FB|Etalons}}) | |||
Exp. Anforderungen bei gewünschter Linienbreite <math>\text{d}{{\nu }_{Laser}}\approx 1\text{MHz}</math> | |||
z. B. <math>\lambda =500\text{nm }\to \nu =6\cdot {{10}^{14}}\text{Hz}\quad \text{d}{{\nu }_{Laser}}/\nu =1,6\cdot {{10}^{-9}}</math> | |||
d. h. Resonatorstabilität <math>dL/L \approx 10^{-9}</math>(bei <math>L = 1 m dL \sim 1</math> nm) | |||
z. B. Temperaturstabilität: d<math>dL/L=\alpha dT\to dT\le {{10}^{-3}}K</math>, mit <math>\alpha </math> Invar z.B. <math>10^{-6}</math>K | |||
Druckabhängigkeit: statt L eigentlich <math>\to n\cdot L</math>, n Brechungsindex | |||
der Luft | |||
<math>n = n(p) \approx 1,0003...</math> für <math>p = p_0 = 1 bar</math> | |||
<math>dL/L\text{ }=\text{ }(n-1)\text{ }dp/{{p}_{0}}\text{ }=3\cdot {{10}^{-4}}dp/{{p}_{0}}\text{ }\to dp\text{ }\le \text{ }3\cdot {{10}^{\text{-6}}}\text{ bar=}3\cdot {{10}^{-3}}\text{ mbar}</math> | |||
Aktuelle Version vom 17. August 2011, 15:18 Uhr

|
Der Artikel Synchrotron- und Laserstrahlung basiert auf der Vorlesungsmitschrift von Moritz Schubotz des 17.Kapitels (Abschnitt 0) der Kern- und Strahlungsphysikvorlesung von Prof. Dr. P. Zimmermann. |
|}}
Die Abfrage enthält eine leere Bedingung.
Wichtigste experimentelle Entwicklungen der letzten 20 Jahre: Speicherringe (Hochenergiephysik) und Laser.
Synchrotronstrahlung
Spektralverteilung der Strahlung
Vertikale Divergenz :
Zeitstruktur:
Im Multi-bunch-Betrieb ca. 100 bunches (1 ~ 3 cm) im Ring von l = 60 m und 500 MHz HF-Sender: 100 ps-Pulse mit 2 ns-Abstand (Umlaufzeit 200 ns)
Laser
Grundgleichungen
Lasertypen:
- Gaslaser: He-Ne, Edelgasionen-Laser (CW), N2-, Excimer-Laser (gepulst)
- Festkörper: Nd:YAG-, Rubin-, Halbleiter-Laser
- Flüssigkeit: Farbstofflaser
Bestimmende Größen:
- Wellenlänge: ,
- Schärfe: ,
- Abstimmbereich: ,
- Divergenz: ,
- Leistung: L
Bei Pulsbetrieb:
- Pulsbreite: ,
- Pulsenergie: E,
- Repetitionsrate
Grundgleichungen:
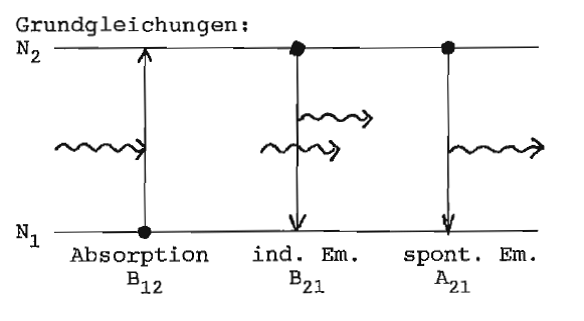
Im thermodynamischen Gleichgewicht:
mit Boltzmann verwenden, nach auflösen und mit Planckschem Strahlungsgesetz vergleichen, ergibt
a) --> Besetzungsinversion notwendig
b) -> -Zunahme der störenden Spontanemission (siehe Röntgenlaserentwicklung)
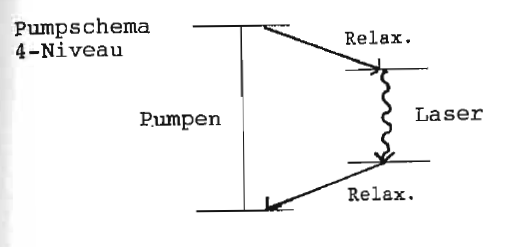
Einige Lasertypen
Verstärkerprofil z. B. Dopplerbreite, Druckverbreiterung, Stöße
Exp. Beispiele:
Einmodenlaser: Stufenweise Einschränkung durch verschiedene optische Filter (Lyot, Etalons)
Exp. Anforderungen bei gewünschter Linienbreite z. B.
d. h. Resonatorstabilität (bei nm)
z. B. Temperaturstabilität: d, mit Invar z.B. K
Druckabhängigkeit: statt L eigentlich , n Brechungsindex der Luft für