Synchrotron- und Laserstrahlung

Kern- und Strahlungsphysikvorlesung von Prof. Dr. P. Zimmermann

Der Artikel Synchrotron- und Laserstrahlung basiert auf der Vorlesungsmitschrift von Moritz Schubotz des 17.Kapitels (Abschnitt 0) der Kern- und Strahlungsphysikvorlesung von Prof. Dr. P. Zimmermann.

   |}}

Die Abfrage enthält eine leere Bedingung.

Wichtigste experimentelle Entwicklungen der letzten 20 Jahre: Speicherringe (Hochenergiephysik) und Laser.

Synchrotronstrahlung

Maxwell-GI., retardierte Potentiale (Relat.theorie) - Schwinger-Gleichungen

Fehler beim Erstellen des Vorschaubildes: Die Miniaturansicht konnte nicht am vorgesehenen Ort gespeichert werden

z.B. 800 MeV, R ~ 1,8 m (BESSY)

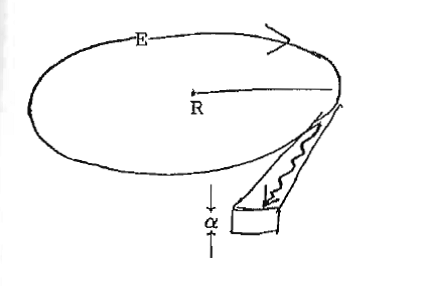
Spektralverteilung der Strahlung

$I(\lambda )\sim (\frac{{\lambda }_c}{\lambda }{)}^4,\lambda \gtrsim {\lambda }_c$

kritische Wellenlänge ${\lambda }_c=\frac{4\pi R}{3{\gamma }^3},\gamma =\frac{E}{m{c}^2}$

BESSY: $R1,8m,E\approx 800MeV\to \gamma \approx 1600:{\lambda }_c\approx 2nm$

Vertikale Divergenz $\alpha$:

$\alpha =\frac{2}{3\gamma }{\left(\frac{\lambda }{{\lambda }_C}\right)}^{1/3}\lambda \gtrsim {\lambda }_C$ z.B. $\lambda =100\text{nm}\to \alpha \approx 1,5\text{mrad}$

Zeitstruktur:

Im Multi-bunch-Betrieb ca. 100 bunches (1 ~ 3 cm) im Ring von l = 60 m und 500 MHz HF-Sender: 100 ps-Pulse mit 2 ns-Abstand (Umlaufzeit 200 ns)

Laser

Grundgleichungen

Lasertypen:

• Gaslaser: He-Ne, Edelgasionen-Laser (CW), N₂-, Excimer-Laser (gepulst)
• Festkörper: Nd:YAG-, Rubin-, Halbleiter-Laser
• Flüssigkeit: Farbstofflaser

Bestimmende Größen:

• Wellenlänge: $\lambda$,
• Schärfe: $d\lambda$,
• Abstimmbereich: $\mathrm{\Delta }\lambda$,
• Divergenz: $d\mathrm{\Omega }$,
• Leistung: L

Bei Pulsbetrieb:

• Pulsbreite: $\mathrm{\Delta }t$,
• Pulsenergie: E,
• Repetitionsrate

Grundgleichungen:

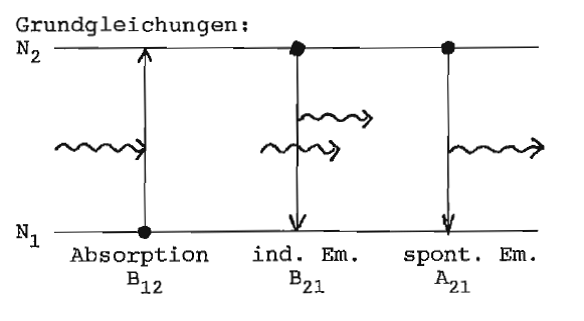
Im thermodynamischen Gleichgewicht:

$A_{21}{N}_2+B_{21}\rho (\gamma )N_2=B_{12}\rho (\gamma )N_1$

mit Boltzmann $N_2/N_1=g_2/g_1\exp (-h\nu /kT)$ verwenden, nach $\rho (\nu )$ auflösen und mit Planckschem Strahlungsgesetz vergleichen, ergibt

a) $g_1{B}_{12}=g_2{B}_{21}$ --> Besetzungsinversion notwendig

b) $A_{21}=B_{21}\frac{8\pi }{c^3}h{\nu }^3$ -> ${\nu }^3$-Zunahme der störenden Spontanemission (siehe Röntgenlaserentwicklung)

Pumpschema 4-Niveau Laser

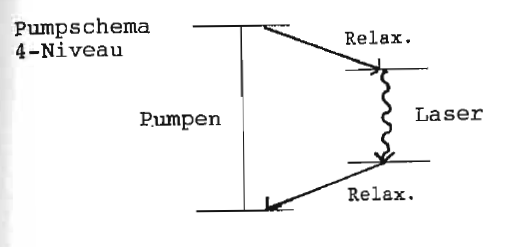
Einige Lasertypen

Fehler beim Erstellen des Vorschaubildes: Die Miniaturansicht konnte nicht am vorgesehenen Ort gespeichert werden

Edelgasionenlaser z. B. Ar⁺- Laser

Excimerlaser z. B. XeCl gepulst, UV 351 - 353 nm 1 - 2 bar He Puffergas, 1 - 10% Xe, 0,2 % HCl, Pulslängen 5 - 15 ns, Repetitionsrate ~ 100 Hz - 1 kHz Impulsenergie ~ J Puls-Leistung 1J/10 ns = 100 MW (Dauerleistung ~ 1 - 100 W)

Nd:YAG-Laser Yttriumaluminiumgranulat $Y_{2}A{l}_5{O}_{12}$ +0,7% Nd: $N{d}^{3+}4d^{10}4f^{3}5s^{2}5p^6$ 4f-Schale durch ss, sp abgeschirmt, Kristallfeldenfluß deshalb relativ gering

Farbstofflaser

Einmodenlaser

Resonator $L=m\frac{\lambda }{2}$, $\lambda =\frac{2L}{m},\nu =\frac{c}{\lambda }=\frac{cm}{2L}$

(longitudinaler) Modenabstand $d\lambda =\frac{2L}{m^2},d\nu =\frac{c}{2L}(=\frac{c}{{\lambda }^2}d\lambda )$

z.B. $L=1\text{m}\to d\nu =\frac{3\cdot {10}^8\text{m/s}}{2\text{m}}=150\text{MHz}$

z.B. $\lambda =500\text{nm}d\lambda =\frac{{\lambda }^2}{c}d\nu =\frac{25\cdot {10}^{-14}{\text{m}}^{\text{2}}}{3\cdot {10}^8\text{m/s}}1,5\cdot {10}^8\text{/s}=1,25\cdot {10}^{-13}\text{m}=0,125\text{pm}=1,25\cdot {10}^{-3}\AA$

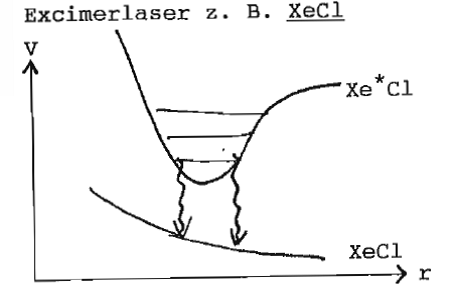
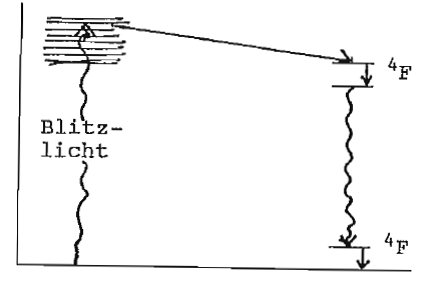
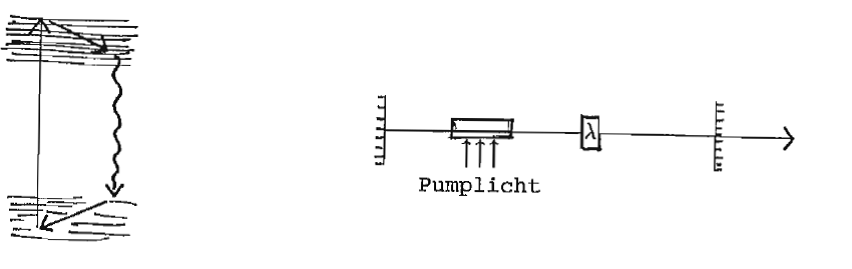
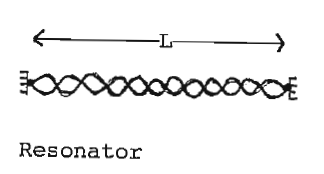
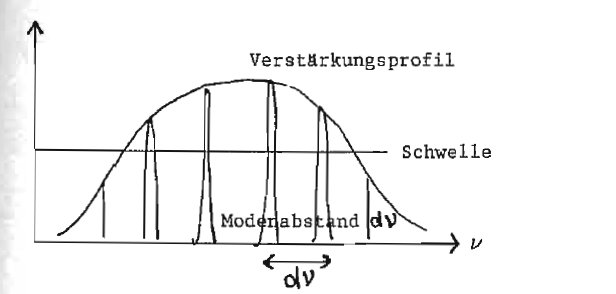
Verstärkerprofil z. B. Dopplerbreite, Druckverbreiterung, Stöße

Dopplerbreite $\frac{\mathrm{\Delta }{\nu }_D}{\nu }=\frac{\mathrm{\Delta }{\lambda }_D}{\lambda }=\frac{v}{c},\frac{v}{c}=\frac{\sqrt{3kT}}{m{c}^2}\approx {10}^{-6}$

z. B. $\lambda =500\text{nm}$ bzw. $\nu =c/\lambda =\frac{3\cdot {10}^8}{5\cdot {10}^{-7}}\text{Hz}=6\cdot {10}^{14}\text{Hz}$

$\begin{array}{rl}& \mathrm{\Delta }{\lambda }_D=0,5\text{pm}\\ & \mathrm{\Delta }{\nu }_D=600\text{MHz}\\ \end{array}$

Exp. Beispiele:

• HeNe $\mathrm{\Delta }{\nu }_D=1500MHz$
• Ar+ $\mathrm{\Delta }{\nu }_D=8000MHz$
• Farbstoff $\mathrm{\Delta }{\nu }_D=103GHz$ (starke Stoßverbreiterung)

Einmodenlaser: Stufenweise Einschränkung durch verschiedene optische Filter (Lyot, Etalons)

Exp. Anforderungen bei gewünschter Linienbreite $\text{d}{\nu }_{Laser}\approx 1\text{MHz}$ z. B. $\lambda =500\text{nm }\to \nu =6\cdot {10}^{14}\text{Hz}\text{d}{\nu }_{Laser}/\nu =1,6\cdot {10}^{-9}$

d. h. Resonatorstabilität $dL/L\approx 10^{-9}$(bei $L=1mdL\sim 1$ nm)

z. B. Temperaturstabilität: d$dL/L=\alpha dT\to dT\le {10}^{-3}K$, mit $\alpha$ Invar z.B. $10^{-6}$K

Druckabhängigkeit: statt L eigentlich $\to n\cdot L$, n Brechungsindex der Luft $n=n(p)\approx 1,0003...$ für $p=p_0=1bar$

$dL/L=(n-1)dp/p_0=3\cdot {10}^{-4}dp/p_0\to dp\le 3\cdot {10}^{\text{-6}}\text{ bar=}3\cdot {10}^{-3}\text{ mbar}$