Aktuelle Version vom 24. August 2011, 17:35 Uhr

Röntgenphysikvorlesung von Prof. Dr. B. Kanngießer

Der Artikel Weiteres zur Röntgenphysik basiert auf der Vorlesungsmitschrift von Moritz Schubotz des 11.Kapitels (Abschnitt 0) der Röntgenphysikvorlesung von Prof. Dr. B. Kanngießer.

|}}

Die Abfrage enthält eine leere Bedingung.

Weiteres zur Röntgenphysik: (Vorlesung 1)

Siehe auch Professor David Attwood (VL1)

Block I

VLV Röntgenfloureszesspektroskopie

Detailliert $K_{α i}, Δ l = \pm 1, Δ j = 0, \pm 1$

LS-Kopplung \Delta S, \Delta L =0, \pm 1

$L = \sum l_{i}, S = \sum s_{i}, J = L + S$ (leichte Atome z.B. Kohlenstoff)

Spin Bahjnk Kopplung für einzelne $e^{-}$ wird aufgehoben

jj-Kopplung $Δ j = 0, \pm 1$ für $e^{-}$ $Δ j = 0$ sonst (z.B. schwerer Atome z.B. Pb (Blei))

$j_{i} = l_{i} + s_{i}, J = \sum j_{i}$ (Kopplung für jedes einzelne $e^{-}$ )

Fundamentalparameter (RFA)

Streuquerschnitt für $h ν$
- atomarer Streuquerschnitt
- linearer Absorptionskoeffizient µ
- Massen Absorptionskoeffizient
Streuquerschnitt für $e^{-}$
Absorptionskanten
Übergangsverhältnisse
Fluoreszenzausbeute:Photoemissionen/Leerstellen (Rest --> Auger-Elektronen)
Elektronenergieniveaus, Energien der Emissionslinien
Übergangswahrscheinlichkeiten --> Fermis-Goldene Regel
Anregungsspektren

Photoabsorption

Photonen
Photo-Elektronen (Photoeffekt)
Auger-Elektronen
Coster-Kronig $L_{1} L_{2} M$
Super-Coster-Kronig $L_{1} L_{2} L_{3}$

lin. Absorption $I (x) = I_{0} \exp (- μ x)$ $μ \propto \frac{ρ Z^{4}}{A E^{3}}$

Quantifizierung von XRF-> Umrechnung XRF-Spektren in Konzentrationen

Methoden: \alpha-Koeffouoent-Methode: empirische Kalibrierung Fundamentalparametermethode theoretische Beziehung zwischen Konzentration und netto Emission Monte Carlo Methode Simulation Vergleich von Simulation mit gemessenen spektren

Mikro RFA Polykapillarlinse im Anregungskanal 3D Mikro RFA Definiert durch Schnitt von Anregungs und Detektionskanal

VLVI Röntgen Beugung

Kristalline Medeien haben periodische Struktur --> Gitterkonstante
Gitterebenen durch sogenannte Millerindizes (ganzzahlige vielfachche von 1/k) beschrieben

Beugung: jedes periodische Element streut kohärent (Konstruktive Interferenz in bestimmtem Winkel)

Elektronen in einem Atom streuen kohärent (Wechselwirkung des elektrischen Feldes mit der Strahlung)

Atome in einem Kristall sind ein Array kohärenter Strahler

Die Wellenlänge von Röntgenlichet liegt in vergleichbarer Größenordnung des Gitterabstands \lambda\approx d

Beugungsmuster enthält Informationen über die Gitterstruktur beziehungsweise den Kristall

Reflexion inkohärenter Streuung, Absorption, Brechung, Transmission bei Materie WW

Bragg Bedingung $n λ = 2 d \sin θ$

Pulverdiffraktometrie

Annahme: stets eine statistiche Anzahl an Ebenen richtig (für konstruktive Interferenz) orientiert

Bragg ist eigentlich kohärente Streuung und nicht Reflektion (Nur Erklärung an Netzebenen

3D-Bragg--> Laue $\underline{a} δ k = n λ$

Bragg Modell

Spiegelnde Reflexion an parallel Netzebenen mit d=const im Kristall

Laue Modell

Kristall als Bravaisgitter (kleinste Einheitszelle) an Gitterpunkten sitzen Atime die kohärent Streuen;

Nur die Richtung kostruktiver Interferenz sieht man Reflexe

Laue Bedingung: Konstruktive Interferenz wenn \delta k beim Streuen reziproken Gittervektoren entspricht

Intensität gestreuter Elektronen

Atomarer Streufaktor: f=(Amplitude der an einem Atom gestreuten Welle)/(Amplitude der an einem Elektron gestreuten Welle)

Strukturfaktor: f=(Amplitude der an allen Atomen einer Einheitszelle gestreuten Welle)/(Amplitude der an einem Elektron gestreuten Welle)

Reziprokes Gitter: Das reziproke Gitter ist der "Kerhwert" der promitiven Einheitszelle

Gitter SC-> Rez. Gitter SC
Gitter BCC-Y Rez. Gitter FCC

Gewichtungsfaktor F²=4f²

Ewald-Kugel: Die reziproken Gitterpunkte sind die Werte des Impulsübertrags für die die Braggleichung erfüllt ist

Für Beugung muss Streuvektor gleich rez Gittervektor gelten

Geometrisceh Wenn der Ursprung des rez. Raums an der Spitze von k liegt, dann findet Beugung genau für die reziproken Gitterpunkte statt, die auf der Ewaldkugel liegen

$n λ = 2 d \sin θ \to \sin θ_{k l m} = \frac{n λ}{2 d_{k l m}} = \frac{n / d_{k l m}}{2 / λ}$ Erkennung der Kristallstruktur

VLVII Compton Streuung

Block II: Erzeugung von Röntgenstrahlung

Überblick:

Röntgenröhre
Synchrotron
FEL (langer Undulator)

Soft X-Ray 500-5KeV

Hard (bis 100KeV)

VL1

X-Ray durch Abbremsung + Absorption von $e^{-}$ mit $E_{k} > 10 k e V$

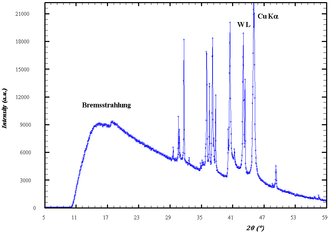
Zahnmedizin 80keV 10 mA --> 800 W

Knochen 170keV 50mA --> 8,5kW

Bremsstrahlung: $Δ E = h ν = E_{K i n, 1} - E_{K i n, 2}$

PC-Monitore Ionisation charakteristische Strahlug $E_{x y} = (x^{- 2} - y^{- 2}) R_{\infty} (Z - X)^{2}$

Bessy II $E_{K i n} = 1, 76 G e V$ $E_{k i n, S y n c} = 500 M e V$ ^[1]

Symbol English Deutsch

A Cathode Kathode

B Deflection coils Ablenk-Spulen

C Cooling-liquid Kühlflüssigkeit

D Motor for rotation Motor für Rotation

E Electron beam Elektronenstrahl

F X-ray windows Austrittsfenster für Röntgenstrahlung

G Anode Anode

siehe auch Röntgenstrahlung

VLII

$B r i l l i a n z = \frac{P h o t o n e n a n z a h l}{s (m m)^{2} (m r a d)^{2} 0, 1 % B W}$

Synchrotronquellen

Anfangs Kreisrund mit Ablenkmagneten

Heute z.B. 8-Eckig mit Wigglern und Undulatoren auf graden Strecken

Ablenkmagnet $F_{L} = q (v \times B) = \dot{p}, p = γ m_{0} v$

$\frac{d^{2} r}{d t^{2}} = - \frac{V^{2}}{R} \to R = \frac{γ m v}{e B} \approx \frac{γ m c}{e B}$

Block III

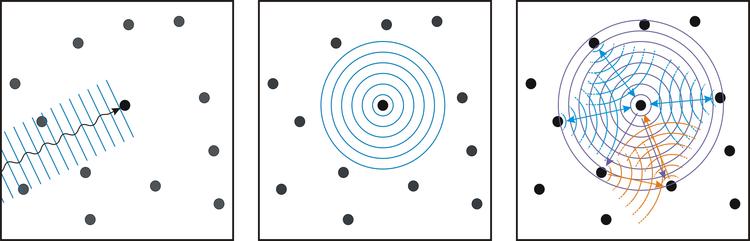
XAFS (NEXAFS/XANES und EXAFS Entstehung, schematisch).
Links: Die einfallende ebene Welle wird von einem Atom absorbiert. Mitte: Das absorbierende Atom emittiert seinerseits eine sphärische Photoelektronenwelle. Rechts: Die emittierte Photoelektronenwelle wird an umliegenden Atomen gestreut. Es kommt dabei einerseits (blau) zu Einfachstreuprozessen die die Ursache für die EXAFS-Strukturen sind, andererseits (orange) kommt es aber auch zu Mehrfachstreuprozessen die die Ursache für die NEXAFS/XANES-Strukturen sind.

Block IV

Quellen

↑ Thomsen,C Gumlich, H.E.: Ein Jahr für die Physik. 3. Auflage Berlin: Wissenschaft und Technik Verliag, 2008, Gleichung {{{2}}} Der für das Attribut „PhIng“ des Datentyps Seite angegebene Wert „{{{2}}}“ enthält ungültige Zeichen oder ist unvollständig. Er kann deshalb während einer Abfrage oder bei einer Annotation unerwartete Ergebnisse verursachen.

[1] Thomsen,C Gumlich, H.E.: Ein Jahr für die Physik. 3. Auflage Berlin: Wissenschaft und Technik Verliag, 2008, Gleichung {{{2}}} Der für das Attribut „PhIng“ des Datentyps Seite angegebene Wert „{{{2}}}“ enthält ungültige Zeichen oder ist unvollständig. Er kann deshalb während einer Abfrage oder bei einer Annotation unerwartete Ergebnisse verursachen.

[1]

@@ Zeile 1: / Zeile 1: @@
-=Zusammenfassung Röntgenphysik SS 11=
+<noinclude>{{ScriptProf|Kapitel=11|Abschnitt=0|Prof=Prof. Dr. B. Kanngießer|Thema=Röntgenphysik|Schreiber=Moritz Schubotz}}</noinclude>
-==Motivation==
+Weiteres zur Röntgenphysik:
-===Größenordnungen===
+(Vorlesung 1)
-Folie II
-[[Datei:Electromagnetic spectrum c.svg|miniatur|hochkant=4|zentriert|Übersicht Wellenlängen]]
-[[File:Electromagnetic Spectrum with Gamma X-Ray NMR Windows-de.svg|miniatur|NMR+XRay]]
-wichtige Größenordnungen:
-*10 eV Extreme Ultraviloet
-*1 KeV Soft X-Rays (~1nm)
-*10 KeV Hard X-Rays
-===Anwendunen für Röntgenstrahlung===
+Siehe auch [http://ast.coe.berkeley.edu//sxreuv/2005/Ch01.pdf Professor David Attwood (VL1)]
-(Folie IV)
-*Bilder von Gewebe und andern Materialien
-*Atom und Molekülstruktur (Aufenthaltsort der Atome)
-*Elektronische Struktur und Bindungen (Aufenthaltsort der Elektronen)
-*Magnetische Eigenschften (Spin)
-==Wechselwirkung elektromanetischer Strahlung mit Materie==
-(Folie VI)
-Monochromatische Anreung
-*Photoelektrische Absorption
-**Photo-Elektronen
-**Auger Elektronen
-**Fluoreszens
-*Streuung
-**Inelastische Streuung
-**Eleastische Streuung
-==Quellen für Röntgenstrahlung==
-==Spektroskopische Methoden==
-==Röntgenbeugungsmethoden==
-=Röntgenphysik II=
 ==Block I==
-===VLI Moderne Röntgenoptiken===
-<math>n=1-\delta+i\beta</math> (2.37)
-{{FB|Snellius}} <math>\frac{\sin \alpha _1 }{\sin\alpha_2}=\frac{n_2}{n_1}\Rightarrow \alpha_c = \sin^{-1}(1-\delta)\approx \frac\pi2-\sqrt{2\delta}</math> (2.52)
-siehe auch Abb 2.7
-<math>\alpha_c\approx0.02\frac\sqrt\rho E</math> mit <math>\rho</math> in <math>g \text{(cm)}^{-3}</math> und E in keV
-====Monokapillarlinsen====
-*zylindrisch oder mit sich verengendem Querschnitt
-* Formen:
-**konisch
-**elliptisch / parabolisch längst Kapillarachse
-<math>\exists</math> (Halb)linsen
-Röntgenlinsen i.A. Kap 3.3 ab S123
-siehe auch [http://www.x-ray-optics.de Seite zu Röntgenoptiken]
-[[File:Xray focus.gif|thumb|Xray focus]]
-===VLII Multilayer===
-<math>n\lambda=2d \sin \theta \sqrt{1-\frac{4\bar\delta d^2}{n^2\lambda^2}}</math>(3.30)
-*n Ordnung
-*d Gesamtdicke einer AB-Lage
-*<math>\bar \delta</math> gemittelter Brechkoeffizent
-Anforderungen:
-*Thermische Stabilität (bei Ausleuchtung)
-*geringe Rauhigkeit
-*geringe Absorption
-[[Datei:Roentgen_Multilayer_Vorkommen.pdf|600px|thumb|zentriert|Abbildungen Att Reflexion optische Gitter im bereich bis 50eV natürliche Kristalle <math>n \lambda=2 d \sin \theta</math> ab 5KeV dazwischen Lücke die durch Multilayer/Vielschichtspiegel geschlossen werden kann]]
-[[Datei:Roentgen_Multilayer.pdf|600px|thumb|zentriert|Abb. 3.23 Schichtaufbau multilayer]]
-===VLIII Streuung Beugung Reflexion===
-Abb 2.1
-<math>\underline{r_e^2}=\frac{e^2}{4\pi\epsilon_0 \underline{m_e c^2}}</math> Selbstenergie (2.14)
-<math>\left(\frac{d\sigma}{d\Omega}\right)_T=r_e^2sin^2\theta</math> (2.15) Streuung an freiem elektron (Thomsen)
-[[File:Dipol Torus.png|thumb|(Abb. 2.2) Abstrahlcharakteristik Dipol, Beschleunigung nach oben Verhalten sin^2 \theta , mit theta winkel zwischen a und Beonbachter <math>\frac{dP}{d\Omega}=\frac{e^2a^2\sin^2\theta}{16 \pi^2\epsilon_0c^3}</math> (2.11)]]
-<math>\left(\frac{d\sigma}{d\Omega}\right)_R=\left(\frac{d\sigma}{d\Omega}\right)_T|f|^2</math> Rutherfordstreuung mit <math>f(\Delta k,\omega)=\omega^2\sum_s(\omega^2-\omega_s^2-i\gamma\omega)^{-1}\exp(i\Delta k \Delta r_s)</math> (2.20) bei Reileigh <math>\omega^4\to \lambda^{-4}</math> --> Himmel blau, <math>\omega_{in}\ll\omega_s \sim (R_a) \to \lambda> R_a</math>
-st order Born Plain Wave approximation (Beobachter weit weg) Abb2.4
-Fernfeld Näherung (Frauenhofer) Spaltfunktion --> FT (Fourieroptik)
-gegensatz Nachfeld Frenel Fresnelsche Zonenplatten
-===VLIV Brechungsindizes===
-;EUV: Extreme Ultraviolett
-;SXR: Soft-X-Ray
-<math>
-\theta_c=\sqrt{2\delta}\propto \lambda \sqrt Z</math>
 ===VLV Röntgenfloureszesspektroskopie===
 Detailliert <math>K_{\alpha i}, \Delta l = \pm 1, \Delta j = 0, \pm 1</math>
@@ Zeile 108: / Zeile 27: @@
 **linearer Absorptionskoeffizient µ
 **Massen Absorptionskoeffizient
-*Streuquerschnitt für e^-
+*Streuquerschnitt für <math>e^-</math>
 *Absorptionskanten
 *Übergangsverhältnisse
 *Fluoreszenzausbeute:Photoemissionen/Leerstellen (Rest --> Auger-Elektronen)
-*Elektronenergieniveaus, Energien der Emissionslinien \vspace{-3mm}
+*Elektronenergieniveaus, Energien der Emissionslinien
 * Übergangswahrscheinlichkeiten --> Fermis-Goldene Regel
 *Anregungsspektren
@@ Zeile 126: / Zeile 45: @@
 *Super-Coster-Kronig <math>L_1L_2L_3</math>
+[[Datei:Atom model for Auger process DE.svg|miniatur|Schematische Darstellung des Auger-Effekts (KLM-Auger-Prozess)]]
 lin. Absorption <math>I(x)=I_0 \exp(-\mu x)</math> <math>\mu \propto  \frac{\rho Z^4}{A E^3}</math>
@@ Zeile 250: / Zeile 170: @@
 ===VLII===
+<math>\rm Brillianz =\frac{\rm Photonenanzahl}{\rm s (mm)^2 (mrad)^2 0,1%BW}</math>
+Synchrotronquellen
+Anfangs Kreisrund mit Ablenkmagneten
+Heute z.B. 8-Eckig mit Wigglern und Undulatoren auf graden Strecken
+Ablenkmagnet <math>F_L=q(v\times B)=\dot p , \quad p=\gamma m_0 v</math>
+<math>\frac{d^2r}{dt^2}=-\frac{V^2}R\to R=\frac{\gamma m v}{eB}\approx\frac{\gamma m c}{e B}</math>
+[[File:Undulator-prinzip.svg|Undulator Prinzip|thumb]]
+[[File:Syncrotron radiation energy flux.png|Syncrotronstrahlung|thumb]]
+[[File:Undulator wih axis.png|thumb|Undulator II]]
-==Block II==
 ==Block III==
-[[File:XAFS.pdf|thumb|XAFS]]
+[[Datei:XAFS.pdf|miniatur|hochkant=2.5|XAFS (NEXAFS/XANES und EXAFS Entstehung, schematisch).<br /><small>Links: Die einfallende ebene Welle wird von einem Atom absorbiert. Mitte: Das absorbierende Atom emittiert seinerseits eine sphärische Photoelektronenwelle. Rechts: Die emittierte Photoelektronenwelle wird an umliegenden Atomen gestreut. Es kommt dabei einerseits (blau) zu Einfachstreuprozessen die die Ursache für die EXAFS-Strukturen sind, andererseits (orange) kommt es aber auch zu Mehrfachstreuprozessen die die Ursache für die NEXAFS/XANES-Strukturen sind.</small>]]
+[[Datei:NEXAFS EXAFS schematic.svg|miniatur|hochkant=1.5|Röntgenabsorptionsspektrum im Bereich einer Absorptionskante (schematisch). Die Kante ist durch einen Pfeil markiert, und der bei EXAFS untersuchte Energiebereich hellblau hinterlegt.]]
 ==Block IV==

Weiteres zur Röntgenphysik: Unterschied zwischen den Versionen

Aktuelle Version vom 24. August 2011, 17:35 Uhr

Inhaltsverzeichnis

Block I

VLV Röntgenfloureszesspektroskopie

VLVI Röntgen Beugung

Pulverdiffraktometrie

Bragg Modell

Laue Modell

VLVII Compton Streuung

Block II: Erzeugung von Röntgenstrahlung

VL1

VLII

Block III

Block IV

Quellen

Navigationsmenü

Symbol	English	Deutsch
A	Cathode	Kathode
B	Deflection coils	Ablenk-Spulen
C	Cooling-liquid	Kühlflüssigkeit
D	Motor for rotation	Motor für Rotation
E	Electron beam	Elektronenstrahl
F	X-ray windows	Austrittsfenster für Röntgenstrahlung
G	Anode	Anode

Weiteres zur Röntgenphysik: Unterschied zwischen den Versionen

Aktuelle Version vom 24. August 2011, 17:35 Uhr

Block I

VLV Röntgenfloureszesspektroskopie

VLVI Röntgen Beugung

Pulverdiffraktometrie

Bragg Modell

Laue Modell

VLVII Compton Streuung

Block II: Erzeugung von Röntgenstrahlung

VL1

VLII

Block III

Block IV

Quellen

Navigationsmenü

Suche