Kernradien

Kern- und Strahlungsphysikvorlesung von Prof. Dr. P. Zimmermann

Der Artikel Kernradien basiert auf der Vorlesungsmitschrift von Moritz Schubotz des 2.Kapitels (Abschnitt 0) der Kern- und Strahlungsphysikvorlesung von Prof. Dr. P. Zimmermann.

   |}}

Die Abfrage enthält eine leere Bedingung.

Kernradienbestimmung durch Streuexperimente mit hochbeschleunigten Elektronen (Hofstadter-Experimente)

Hofstadter-Experimente

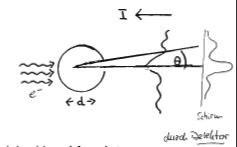
Beugungsmaxima und -minima

Erstes Minimum bei $\sin \theta \approx 0,61\frac{\lambda }{d}$

Bedingung: $\lambda \le d$

Für Kern $\lambda \le 10^{-14}m$, als 'Licht' sind hochbeschleunigte Elektronen gut geeignet (keine Starke WW).

Verknüpfung von Energie E, Impuls p und Wellenlänge $\lambda$ durch relativistische Energiegleichung:

Einstein Energiegleichung

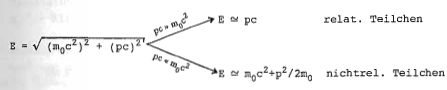
Für relat. Teilchen ($E\gg m_0{c}^2$, exakt für Teilchen mit Ruhemasse $m_0=0$, d.h. Photonen, Neutrinos (?), Gravitonen (?), ... ) gilt wegen $E=pc$ für die de Broglie-Wellenlänge $\lambda {}^{-}$:

$\lambda {}^{-}=\frac{\hslash }{p}=\frac{hc}{E}\approx \frac{3\times 10^{8-34}m}{1.6\times 10^{-19+6}E[MeV]}\approx 200\frac{10^{-15}}{E[MeV]}$

d.h. für $E>200MeV$ ist $\lambda {}^{-}<10^{-15}m$.

Hofstädter-Experimente am Linearbeschleuniger in Stanford 1957

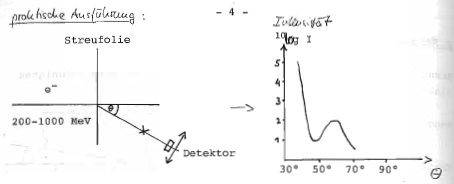
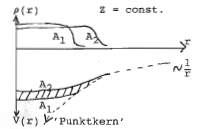
Ergebnis der Messungen für viele Elemente: $R\approx A^{1/3}=1,20A^{1/3}10^{-15}m$

Genauer: kein scharfer Rand

Für alle Kerne etwa gleiche Ladungsdichte ${\rho }_0$ im Inneren und gleiche Randbreite von ca. $2\times 10^{-15}$ m.

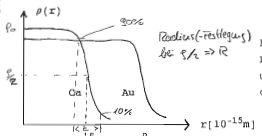
Quantitativ beschreibbar durch die Wood-Saxon-Formel:

$\rho (r)=\frac{{\rho }_0}{1+\exp \frac{r-R}{a}}$

Randbreite (90% $\to$ 10% Abfall) $\approx 4,40a\approx 2,4\times 10^{-15}m$ 'Radius' $R=1,07\times A^{1/3}10^{-15}$ m

Andere Meßmethoden zur Kernradienbestimmung: Isotopieverschiebung (Volumeneffekt) im optischen Bereich

besonders für S-Elektronen wegen deren endlicher Aufenthaltswahrscheinlichkeit am Kernort. Noch wesentlich stärkerer Effekt bei myonischen Atomen wegen der ca. 200x kleineren Bahnradien.

Weitere Informationen

(gehört nicht zum Skript) Hofstäder-Experiment