Abschirmung radioaktiver Strahlung: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (9 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
<noinclude>{{ScriptProf|Kapitel=10|Abschnitt=0|Prof=Prof. Dr. P. Zimmermann|Thema=Kern- und Strahlungsphysik|Schreiber=Moritz Schubotz}}</noinclude> | <noinclude>{{ScriptProf|Kapitel=10|Abschnitt=0|Prof=Prof. Dr. P. Zimmermann|Thema=Kern- und Strahlungsphysik|Schreiber=Moritz Schubotz}}</noinclude> | ||
== Abbremsung geladener Teilchen (Bethe-Bloch- | == Abbremsung geladener Teilchen (Bethe-Bloch-Formel) == | ||
[[Datei:10.1.Bethe-Bloch-Formel.png]] | [[Datei:10.1.Bethe-Bloch-Formel.png|miniatur|zentriert|hochkant=4|Abbremsung geladener Teilchen]] | ||
Übertragener Impuls | |||
(senkrecht zur Flugrichtung) | Übertragener '''Impuls''' (senkrecht zur Flugrichtung) | ||
:<math>P_\bot = \text{Kraft} \times \text{Stosszeit}\approx\frac{1}{4\pi\epsilon_0}\frac{Ze^2}{b^2}\frac{b}{v}</math> | |||
Übertragene Energie E = | |||
Übertragene '''Energie''' <math>E = \frac{p^2}{2m} \approx \frac{1}{4\pi\epsilon_0}^2 \frac{Z^2 e^4}{b^2 v^2 m}</math> | |||
Summation über alle Elektronen mit {{FB|Stoßparameter}} zwischen b und | |||
b + db ergibt Faktor <math>2\pi b db N</math> (N Dichte der Elektronen, im Festkörper | |||
Summation über alle Elektronen mit Stoßparameter zwischen | ist N ~ <math>\rho</math>). | ||
b + db ergibt Faktor 2 | |||
ist N ~ | |||
Intergration über alle Stoßparameter zwischen | Intergration über alle Stoßparameter zwischen b<sub>max</sub> und b<sub>min</sub> ergibt | ||
Energieverlust pro Wegstrecke dx | Energieverlust pro Wegstrecke dx | ||
dE | {{Gln| | ||
<math>\frac{dE}{dx}=\int_{b_{min}}^{b_{max}} \frac{1}{4\pi\epsilon_0}^2 \frac{Z^2 e^4 2 \pi N}{m v^2} \frac{1}{b} db =\frac{1}{4\pi\epsilon_0}^2 \frac{Z^2 e^4 2 \pi N}{m v^2} \ln \frac{b_{max}}{b_{min}}</math>|Energieverlust pro Wegstrecke}} | |||
Wichtiger Faktor: | |||
v 2 | |||
Wichtiger Faktor:<math>\frac{Z^2 N}{v^2}</math> | |||
Obere und untere Grenze: | Obere und untere Grenze: | ||
:<math>b_{min} \succsim \bar \lambda = \frac{\hbar}{mv}</math> {{FB|de Broglie Wellenlänge}} des Elektrons vom Ruhesystem des ion. Teilchens aus gesehen | |||
des ion. Teilchens aus gesehen | |||
b<sub>max</sub>: Stoßzeit b<sub>max</sub>/v kleiner als mittlere Umlaufzeit des Atomelektrons, d. h. <math>b_max/v \succsim 1/\tilde{\nu} \quad b_max\le v/\tilde \nu </math> | |||
:<math>\frac{b_{max}}{b_{min}}\approx \ln \frac{mv^2}{h\tilde \nu}\approx \ln \frac{mv^2}{<I>}</math> | |||
d. h. | |||
<nowiki><I></nowiki> mittleres {{FB|Ionisationspotential}} grob: <math><I> \approx 12 eV Z_{Absorber}</math> | |||
grob: <I> | |||
Genauere Rechnung mit relativistischen Termen (besonders wichtig | Genauere Rechnung mit '''relativistischen''' Termen (besonders wichtig | ||
für ion. Elektronen, da diese schon im MeV-Bereich relat. zu behandeln | für ion. Elektronen, da diese schon im MeV-Bereich relat. zu behandeln | ||
sind). | sind). | ||
[[Datei:10.2.Graph.Bethe-Bloch.png|miniatur|zentriert|hochkant=3|Allgemeine Form von dE/dx]] | |||
[[Datei:10.2.Graph.Bethe-Bloch.png]] | |||
Energieverlust von e-, p und | Energieverlust von e<sup>-</sup>, p und <math>\alpha</math> in Luft (<math>\rho \approx 1,2 mg/cm^3</math> ) | ||
E[ | [[Datei:10.3.Tabelle.Bethe-Bloch.png|miniatur|zentriert|hochkant=3]] | ||
Damit Reichweiten Luft Festkörper | |||
z. B. <math>E \approx 1</math> MeV | |||
[[Datei:10.4.alpha.beta.reichweiten.png|miniatur|hochkant=2|Reichweiten]] | |||
==Absorption von Gamma-Strahlung== | |||
[[Datei:10.3. | |||
{{FB|Photoeffekt}} - {{FB|Compton-Effekt}} - {{FB|Paarbildung}} | |||
===Photoeffekt=== | |||
<math>\hbar \omega</math> gebundenes Atomelektron (insbes. die 1s-Elektronen) --> freies Elektron mit <math>e = \hbar \omega</math>-Bindungsenergie des Elektrons | |||
(hohe Abhängigkeit des Wirkungsquerschnitts von Z<sub>Absorber</sub> mit ca. Z<sup>5</sup>) | |||
===Compton-Effekt=== | |||
<math>\hbar \omega+e^-</math> (als freies Elektron betrachtet) --> <math>\hbar \omega'</math> 'Stoß', {{FB|Klein-Nishina-Formel}} | |||
===Paarbildung=== | |||
ab 1 MeV | |||
<math>\hbar \omega \underset{_{\text{+ Kerncoulombpotential}}}{\mathop{\to }}\,{{e}^{+}}+{{e}^{-}}</math> | |||
;grob: {{FB|Photoeffekt}} im keV-Bereich, {{FB|Comptoneffekt}} im MeV-Bereich und {{FB|Paarbildung}} ab ca. 10 MeV entscheidend | |||
;genauer: Wegen der hohen Z-Abhängigkeit von Photoeffekt und Paarbildung ist der relative Beitrag zur <math>\gamma</math>-Abschwächung verschieden (s. Diagramme für C und Pb) | |||
Relativer Beitrag zur <math>\gamma</math>-Abschwächung | |||
[[Datei:10.5.gamma.abschwaechung.effekt.kohlenstoff.png|miniatur|zentriert|hochkant=3|Kohlenstoff]] | |||
[[Datei:10.6.gamma.abschwaechung.effekt.blei.png|miniatur|zentriert|hochkant=3|Blei]] | |||
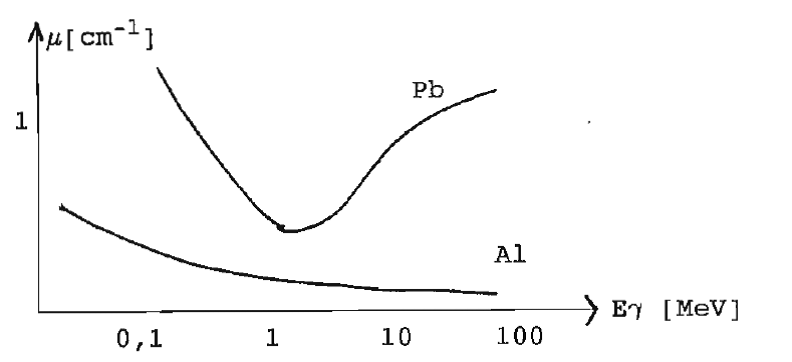
Abschwächungskoeffizient µ = µ(Photo) + µ(Compton) + µ(Paar) | |||
[[Datei:10.7.abschwaechung.intensitaet.png|miniatur|zentriert|hochkant=3]] | |||
[[Datei:10.8.abschwaechung.gamma.Al.Pb.png|miniatur|zentriert|hochkant=3]] | |||
[[Datei:10.9.reichweite.gamma.vergleich.png|miniatur|hochkant=3|z.B. <math>E_\gamma</math> = 1 MeV]] | |||
== Neutronen == | |||
# Schnelle n abbremsen: nach Stoßkinematik am besten durch Kernstöße mit leichten Kernen, z. B. H<sub>2</sub>0, Graphit, Paraffin | |||
# Absorption: besonders gut bei thermischen n durch Cadmium (Cd<sup>113<sup> , 13% im nat. Gemisch) mit d<sub>l/l0</sub> = 0,18 mm | |||
Betonabschirmung <math>\rho=2,3kg/dm^3</math> | |||
{| class="wikitable" | |||
|- | |||
! En [MeV] !! d<sub>l/l0</sub> [ cm] | |||
|- | |||
| 1|| 8 | |||
|- | |||
| 10|| 28 | |||
|- | |||
| 100|| 80 | |||
|} | |||
Aktuelle Version vom 1. Juni 2011, 22:49 Uhr

|
Der Artikel Abschirmung radioaktiver Strahlung basiert auf der Vorlesungsmitschrift von Moritz Schubotz des 10.Kapitels (Abschnitt 0) der Kern- und Strahlungsphysikvorlesung von Prof. Dr. P. Zimmermann. |
|}}
Die Abfrage enthält eine leere Bedingung.
Abbremsung geladener Teilchen (Bethe-Bloch-Formel)
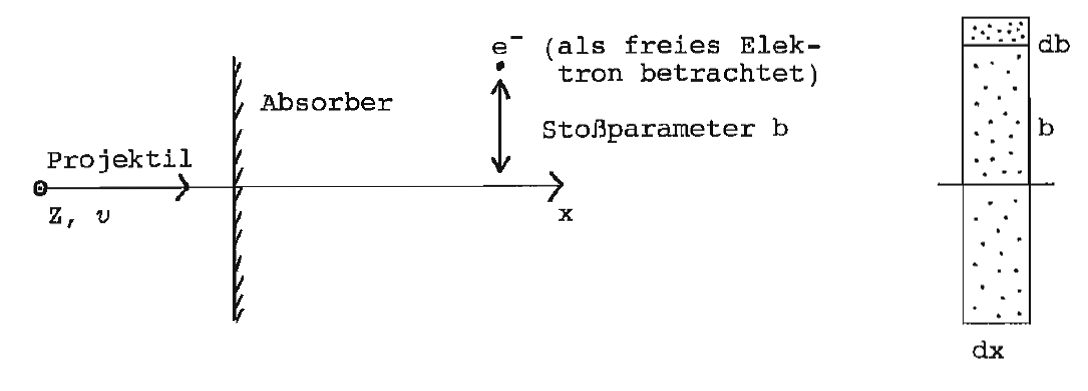
Übertragener Impuls (senkrecht zur Flugrichtung)
Summation über alle Elektronen mit Stoßparameter zwischen b und
b + db ergibt Faktor (N Dichte der Elektronen, im Festkörper
ist N ~ ).
Intergration über alle Stoßparameter zwischen bmax und bmin ergibt
Energieverlust pro Wegstrecke dx
Obere und untere Grenze:
- de Broglie Wellenlänge des Elektrons vom Ruhesystem des ion. Teilchens aus gesehen
bmax: Stoßzeit bmax/v kleiner als mittlere Umlaufzeit des Atomelektrons, d. h.
<I> mittleres Ionisationspotential grob:
Genauere Rechnung mit relativistischen Termen (besonders wichtig
für ion. Elektronen, da diese schon im MeV-Bereich relat. zu behandeln
sind).
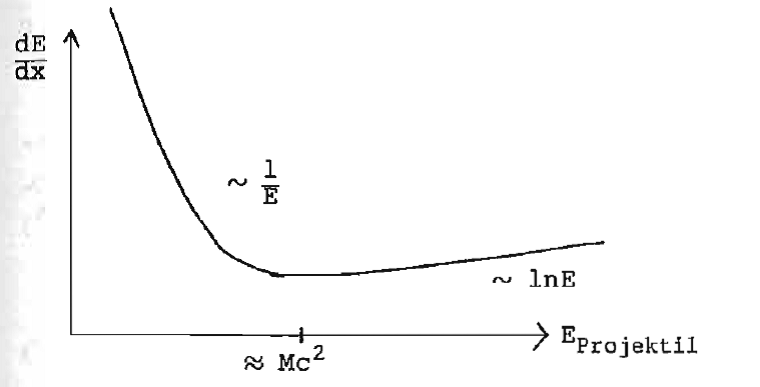
Energieverlust von e-, p und in Luft ( )
Damit Reichweiten Luft Festkörper z. B. MeV

Absorption von Gamma-Strahlung
Photoeffekt - Compton-Effekt - Paarbildung
Photoeffekt
gebundenes Atomelektron (insbes. die 1s-Elektronen) --> freies Elektron mit -Bindungsenergie des Elektrons
(hohe Abhängigkeit des Wirkungsquerschnitts von ZAbsorber mit ca. Z5)
Compton-Effekt
(als freies Elektron betrachtet) --> 'Stoß', Klein-Nishina-Formel
Paarbildung
ab 1 MeV
- grob
- Photoeffekt im keV-Bereich, Comptoneffekt im MeV-Bereich und Paarbildung ab ca. 10 MeV entscheidend
- genauer
- Wegen der hohen Z-Abhängigkeit von Photoeffekt und Paarbildung ist der relative Beitrag zur -Abschwächung verschieden (s. Diagramme für C und Pb)
Relativer Beitrag zur -Abschwächung
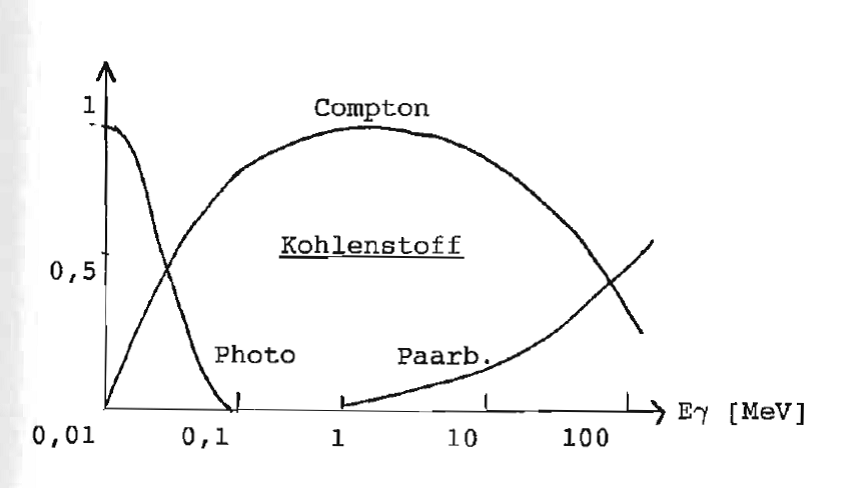
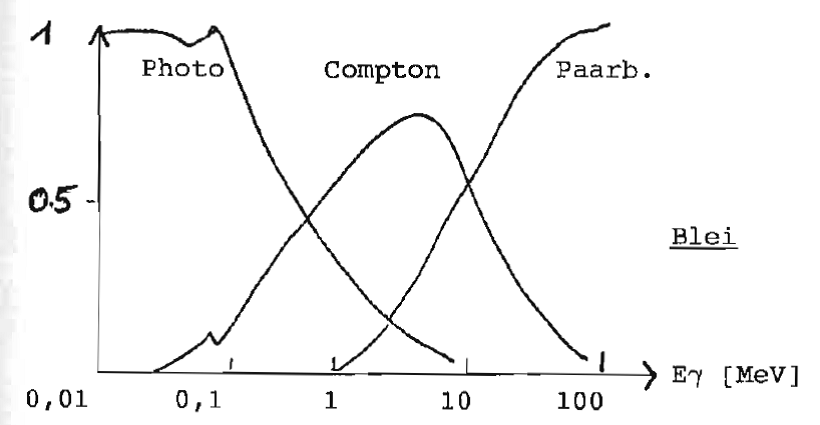
Abschwächungskoeffizient µ = µ(Photo) + µ(Compton) + µ(Paar)


Neutronen
- Schnelle n abbremsen: nach Stoßkinematik am besten durch Kernstöße mit leichten Kernen, z. B. H20, Graphit, Paraffin
- Absorption: besonders gut bei thermischen n durch Cadmium (Cd113 , 13% im nat. Gemisch) mit dl/l0 = 0,18 mm
| En [MeV] | dl/l0 [ cm] |
|---|---|
| 1 | 8 |
| 10 | 28 |
| 100 | 80 |