Beta-Zerfall: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (6 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
<noinclude>{{ScriptProf|Kapitel=12|Abschnitt=0|Prof=Prof. Dr. P. Zimmermann|Thema=Kern- und Strahlungsphysik|Schreiber=Moritz Schubotz}}</noinclude> | <noinclude>{{ScriptProf|Kapitel=12|Abschnitt=0|Prof=Prof. Dr. P. Zimmermann|Thema=Kern- und Strahlungsphysik|Schreiber=Moritz Schubotz}}</noinclude> | ||
:<math>\begin{align} | |||
& \left( A,Z \right)&\to& \left( A,Z+1 \right)+{{e}^{-}}+\bar{\nu }&{{\beta }^{-}}-\text{Zerfall} \\ | |||
& \left( A,Z \right)&\to& \left( A,Z-1 \right)+{{e}^{+}}+\nu &{{\beta }^{+}}-\text{Zerfall} \\ | |||
& {{e}^{-}}+\left( A,Z \right)&\to& \left( A,Z-1 \right)+{{e}^{-}}+\nu &{{e}^{-}}-\text{Einfang} \\ | |||
\end{align}</math> wobei <math>{{\beta }^{+}}</math>-Zerfall und <math>e^-</math>-Einfang sind konkurrierende Vorgänge | |||
reduziert formuliert als | reduziert formuliert als | ||
n | :<math>\begin{align} | ||
& n&\to& p+{{e}^{-}}+\bar{\nu }&{{\beta }^{-}}-\text{Zerfall} \\ | |||
p | & p&\to& n+{{e}^{+}}+\nu&{{\beta }^{+}}-\text{Zerfall} \\ | ||
e- + p | & {{e}^{-}}+p&\to& n+{{e}^{-}}+\nu &{{e}^{-}}-\text{Einfang} \\ | ||
- | \end{align}</math> | ||
Beta-Zerfall energetisch möglich --> siehe {{FB|Isobarenregel}} als Folgerung aus der [[Tröpfchenmodell,_Weizsäckersche_Massenformel#I._Isobarenregeln|Weizsäckerschen Massenformel]] | |||
[[Datei:13.2.beta.fermi.ansatz.png | [[Datei:13.1.beta.messung.png|miniatur|hochkant=3|zentriert|Schema beta Strahlung]] | ||
Beim ß-Zerfall ist neben der {{FB|Halbwertzeit}} <math>t_{1/2} = \frac{0,69}{\lambda}</math> das Energie bzw. {{FB|Impulsspektrum der Elektronen}} (Positronen) meßbar. Ein theoretischer Ansatz muß die Form des Impulsspektrums <math>\lambda(p_e)</math>, d. h. die Wahrscheinlichkeit für die Emission eines Elektrons (Positrons) mit dem Impuls <math>p_e</math> wiedergeben. Die Intergration über alle <math>\lambda(p_e)</math> ergibt | |||
die {{FB|Gesamtübergangswahrscheinlichkeit}} <math>\lambda=\int \lambda(p_e)d p_e </math> und damit | |||
die Halbwertzeit <math>t_{1/ 2}</math>. | |||
Fermi-Ansatz <ref>Z. Physik 88, 161 (1934)</ref> in Analogie zu elektromagnetischen | |||
Übergängen. Störungstheorie ([[Fermis Goldene Regel]]) | |||
:<math>\lambda =\frac{2\pi }{h}{{\left| {{\mathcal{H}}_{if}} \right|}^{2}}\frac{dN}{d{{E}_{0}}}</math> mit | |||
*Wechselwirkungsoperator <math>\mathcal{H}</math>: <math><{{\mathcal{H}}_{if}}>=\int {{\psi }_{f}}\mathcal{H}{{\psi }_{i}}d\tau </math> | |||
*Dichte der Endzustände dN/dE<sub>0</sub> | |||
[[Datei:13.2.beta.fermi.ansatz.png|miniatur|Fermi-Ansatz | |||
<math>\lambda =\frac{2\pi }{h}{{\left| {{\mathcal{H}}_{if}} \right|}^{2}}\frac{dN}{d{{E}_{0}}}</math> | |||
Störungstheorie (Fermi Goldene Regel) | Störungstheorie (Fermi Goldene Regel) | ||
]] | |||
< | :<math><{{\mathcal{H}}_{if}}>=\int \Phi _{\nu }^{*}\left( {{P}_{\nu }} \right)\Phi _{e}^{*}\left( {{P}_{e}} \right)\Phi _{f}^{{}}\left( A,Z+1 \right)\mathcal{H}\Phi _{i}^{{}}\left( A,Z \right)d\tau </math> mit | ||
Leptonen- | *<math>\Phi _{\nu }^{*}\left( {{P}_{\nu }} \right)\Phi _{e}^{*}\left( {{P}_{e}} \right)</math>-Leptonen- Wellenfunktion | ||
(Integration wegen Nukleonen-WF nur über das Kernvolumen) | *<math>\Phi _{f}^{{}}\left( A,Z+1 \right)\Phi _{i}^{{}}\left( A,Z \right)</math>-Nukleonen Wellenfunktion | ||
Bei Leptonen-WF Ansatz freier Teilchen, d. h. auslaufende ebene | *(Integration wegen Nukleonen-WF nur über das Kernvolumen) | ||
kann man zunächst alle Anteile mit | Bei Leptonen-WF Ansatz freier Teilchen, d. h. auslaufende ebene Wellen | ||
da für | <math>\Phi \left( \overrightarrow{p} \right)\tilde{\ }{{e}^{i\left( \vec{p}\vec{r} \right)/\hbar }}=1+i\left( \vec{p}\vec{r} \right)/\hbar -\frac{1}{2}{{\left( \left( \vec{p}\vec{r} \right)/\hbar \right)}^{2}}+\ldots </math> | ||
und damit pR/ | |||
Bei der Integration kann man zunächst alle Anteile mit <math>\left( \vec{p}\vec{r} \right)/\hbar </math> vernachlässigen, da für <math>{{E}_{e}}\succsim 1MeV</math> und für alle <math>E_\nu</math> gilt: | |||
:<math>\hbar/p = \bar \lambda K\approx 200\times10^{-15}m/E[MeV]</math> | |||
und damit <math>pR/\hbar \approx 10^{-2}</math>. Man betrachtet die Leptonenwellenfunktionen | |||
also als konstant im Bereich des Kernvolumens. Diese Näherung ist | also als konstant im Bereich des Kernvolumens. Diese Näherung ist | ||
gleichbedeutend mit der Annahme, daß bei der Leptonenemission kein | gleichbedeutend mit der Annahme, daß bei der {{FB|Leptonenemission}} kein | ||
Bahndrehimpuls weggetragen wird ("erlaubte" Übergänge. | {{FB|Bahndrehimpuls} weggetragen wird ("erlaubte" Übergänge. <math>\Delta l = 0</math>). | ||
"klassische" Deutung | |||
[[Datei:13.3.beta.klassische.deutung.png|miniatur|"klassische" Deutung | |||
QM | |||
<math>L=Rp\overset{\text{QM}}{\mathop{=}}\,\,n\hbar </math> | |||
Bei pR/ | |||
Bei <math>pR/\hbar \ll 1</math> ist nur n = 0 maßgebend | |||
]] | |||
Den | Den Wechselwirkungsoperator ersetzt man durch die Kopplungskonstante g, so daß | ||
g, so daß << | <math>\left\langle {{\mathcal{H}}_{if}} \right\rangle </math> | ||
insgesamt unabhängig von p<sub>e</sub> wird und die Abhängigkeit | |||
des Impulsspektrums allein im statistischen Faktor | des Impulsspektrums allein im statistischen Faktor | ||
dN/ | <math>dN/dE_0</math> (der Dichte der Endzustände) steckt. | ||
Allgemein bei freien Teilchen dN ~ | |||
Emission beider Leptonen dN ~ dN( | Allgemein bei freien Teilchen <math>dN ~ p^2 dp</math>, somit bei gleichzeitiger | ||
Emission beider Leptonen <math>dN ~ dN(p_e)dN(p_\nu)</math> mit <math>E_0 = E_l + E_\nu = | |||
Impulsspektrum | \sqrt{(m_0c^2)^2+(p_ec)^2}+ p_\nu c</math> (Neutrinomasse = 0 gesetzt). Damit wird das | ||
[[Datei:13.4.extrapolation.fermi.darstellung.png]] | Impulsspektrum <math>\lambda(p_e)dp_e</math>: | ||
Durch Extrapolation bei der Fermi-Darstellung Bestimmung von | :<math>\lambda \left( {{p}_{e}} \right)d{{p}_{e}}\tilde{\ }\frac{dN}{d{{E}_{0}}}\tilde{\ }\frac{p_{e}^{2}d{{p}_{e}}p_{\nu }^{2}d{{p}_{\nu }}}{d{{E}_{0}}}\tilde{\ }p_{e}^{2}{{\left( {{E}_{0}}-{{E}_{e}} \right)}^{2}}d{{p}_{e}}</math> wegen | ||
<math>p_{\nu }^{2}={{\left( {{E}_{0}}-{{E}_{e}} \right)}^{2}}/{{c}^{2}}</math> und | |||
<math>\frac{d{{p}_{\nu }}}{dE}=\frac{1}{c}</math> | |||
[[Datei:13.4.extrapolation.fermi.darstellung.png|miniatur|zentriert|hochkant=4]] | |||
Durch Extrapolation bei der {{FB|Fermi-Darstellung}} Bestimmung von <math>E_0</math>. | |||
Damit auch die Möglichkeit zur Bestimmung einer möglichen Neutrinomasse, | Damit auch die Möglichkeit zur Bestimmung einer möglichen Neutrinomasse, | ||
deren Existenz einen großen Einfluß auf Struktur und Entwicklung | deren Existenz einen großen Einfluß auf Struktur und Entwicklung | ||
des Universums hat. Dabei wegen Fehlerabschätzung | des Universums hat. Dabei wegen Fehlerabschätzung E<sub>0</sub> möglichst | ||
klein wählen, z. B. Tritium-Zerfall 3H | klein wählen, z. B. Tritium-Zerfall<math> ^3H \to ^3He + e- + \bar \nu</math> mit | ||
<math>E_0 = 18 keV (t_{1 /2} \approx 12a)</math> [<math>m_\nu c^2</math> zur Zeit <math>\le 7eV</math>]. | |||
Integration über Impulsspektrum: | Integration über Impulsspektrum: | ||
:<math>\lambda =\frac{\ln 2}{{{t}_{{}^{1}\!\!\diagup\!\!{}_{2}\;}}}=\mathop{\int }_{0}^{{{P}_{0}}}\lambda \left( {{p}_{e}} \right)d{{p}_{e}}=\text{const }f(Z,{{E}_{0}})\text{ }</math> mit f ( Z, E<sub>0<sub>) über Coulomb-Korrekturfaktor | |||
\ = | |||
f ( Z, | Die f-Werte sind tabelliert <ref> Feenburg, Trigg, Rev. Mod. | ||
Phys. 22, 399</ref>. Sie enthalten die gesamte Energieabhängigkeit. | |||
Die f-Werte sind tabelliert | |||
Phys. 22, 399 | |||
Grobe Abschätzung: | Grobe Abschätzung: | ||
;nichtrelat. Bereich: (Eo « 1 MeV) : <math>E_e ~ p_e^2\to</math> | |||
nichtrelat. Bereich (Eo « 1 MeV) : | <math>f\tilde{\ }\int p_{e}^{6}d{{p}_{e}}\tilde{\ }p_{0}^{7}\tilde{\ }E_{0}^{3,5}</math> | ||
> | ;relat. Bereich (EO > 1 MeV):<math>E_e ~ p_e^2\to</math> | ||
<math>f\tilde{\ }\int p_{e}^{4}d{{p}_{e}}\tilde{\ }p_{0}^{5}\tilde{\ }E_{0}^{5}</math> | |||
relat. Bereich (EO | |||
Bei genauerer Betrachtung muß man berücksichtigen, daß die Spins | Bei genauerer Betrachtung muß man berücksichtigen, daß die Spins | ||
der beiden Leptonen parallel (Gamow-Teller- | der beiden Leptonen parallel ({{FB|Gamow-Teller-Übergänge}}) oder antiparallel | ||
(Fermi-Übergänge) stehen können. Für erlaubte Übergänge | ({{FB|Fermi-Übergänge}}) stehen können. Für erlaubte Übergänge | ||
( | (<math>\Delta l = 0</math>) gelten somit die Auswahlregeln: | ||
;Fermi-Ü: <math>{{I}_{i}}={{I}_{f}}\to \Delta I=0</math> | |||
Gamow-Teller-Ü: I i = I f + 1 | ;Gamow-Teller-Ü: <math>{{I}_{i}}={{I}_{f}}+1\to \Delta I=0,\pm 1</math> | ||
anschaulich: | anschaulich: | ||
<math>\begin{align} | |||
& \Uparrow &\to &\Uparrow +&\Uparrow +&\Downarrow &\text{Fermi} \\ | |||
Verbotene Übergänge: | & n&\to &p+&{{e}^{-}}+&\bar{\nu } & \\ | ||
Merkmal: größere Drehimpulsänderungen, größere | & \Uparrow &\to &\Downarrow +&\Uparrow +&\Uparrow &\text{Gamow-Teller} \\ | ||
\end{align}</math> | |||
===Verbotene Übergänge:=== | |||
Merkmal: größere Drehimpulsänderungen, größere ft<sub>1/ 2</sub>-Werte | |||
Beiträge für diese Übergänge aus: | Beiträge für diese Übergänge aus: | ||
a) Reihenentwicklung der Leptonenwellenfunktionen | a) Reihenentwicklung der Leptonenwellenfunktionen | ||
e ipr / | |||
<math>{{e}^{ipr/\hbar }}=1+\underbrace{i\left( pr/\hbar \right)-1/2{{\left( pr/\hbar \right)}^{2}}}_{\text{bisher vernachl }\!\!\ddot{\mathrm{a}}\!\!\text{ ssigt}}</math> | |||
b) relativistische Wellenfunktionen der Nukleonen mit | b) relativistische Wellenfunktionen der Nukleonen mit v<sub>N</sub>/c-Beiträge | ||
Beispiele für erlaubte und verbotene Übergänge: | Beispiele für erlaubte und verbotene Übergänge: | ||
[[Datei:13.5.verbotene.uebergaenge.png]] | [[Datei:13.5.verbotene.uebergaenge.png|miniatur|hochkant=4|zentriert]] | ||
==Einzelnachweise== | |||
<references /> | |||
==Weitere Informationen== | |||
(gehört nicht zum Skript) | |||
===Prüfungsfragen=== | |||
*ß Übergänge: Prinzipielle Reaktionsgleichung + Bethe-Weizsäcker | |||
*Neutrinos: Was ist das wozu braucht man die (beim ß Zerfall) | |||
*Besonderheit beim ß Zerfall? (siehe Kapitel Paritätsverletzung) | |||
* Übergangsraten aus Fermis goldener Regel ("grobe" Herleitung) | |||
** Fermi- und GT-Übergänge | |||
Aktuelle Version vom 28. August 2011, 15:36 Uhr

|
Der Artikel Beta-Zerfall basiert auf der Vorlesungsmitschrift von Moritz Schubotz des 12.Kapitels (Abschnitt 0) der Kern- und Strahlungsphysikvorlesung von Prof. Dr. P. Zimmermann. |
|}}
Die Abfrage enthält eine leere Bedingung.
reduziert formuliert als
Beta-Zerfall energetisch möglich --> siehe Isobarenregel als Folgerung aus der Weizsäckerschen Massenformel
Beim ß-Zerfall ist neben der Halbwertzeit das Energie bzw. Impulsspektrum der Elektronen (Positronen) meßbar. Ein theoretischer Ansatz muß die Form des Impulsspektrums , d. h. die Wahrscheinlichkeit für die Emission eines Elektrons (Positrons) mit dem Impuls wiedergeben. Die Intergration über alle ergibt die Gesamtübergangswahrscheinlichkeit und damit die Halbwertzeit .
Fermi-Ansatz [1] in Analogie zu elektromagnetischen
Übergängen. Störungstheorie (Fermis Goldene Regel)
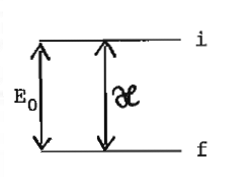
- -Leptonen- Wellenfunktion
- -Nukleonen Wellenfunktion
- (Integration wegen Nukleonen-WF nur über das Kernvolumen)
Bei Leptonen-WF Ansatz freier Teilchen, d. h. auslaufende ebene Wellen
Bei der Integration kann man zunächst alle Anteile mit vernachlässigen, da für und für alle gilt:
und damit . Man betrachtet die Leptonenwellenfunktionen also als konstant im Bereich des Kernvolumens. Diese Näherung ist gleichbedeutend mit der Annahme, daß bei der Leptonenemission kein {{FB|Bahndrehimpuls} weggetragen wird ("erlaubte" Übergänge. ).
Den Wechselwirkungsoperator ersetzt man durch die Kopplungskonstante g, so daß insgesamt unabhängig von pe wird und die Abhängigkeit des Impulsspektrums allein im statistischen Faktor (der Dichte der Endzustände) steckt.
Allgemein bei freien Teilchen , somit bei gleichzeitiger Emission beider Leptonen mit (Neutrinomasse = 0 gesetzt). Damit wird das Impulsspektrum :
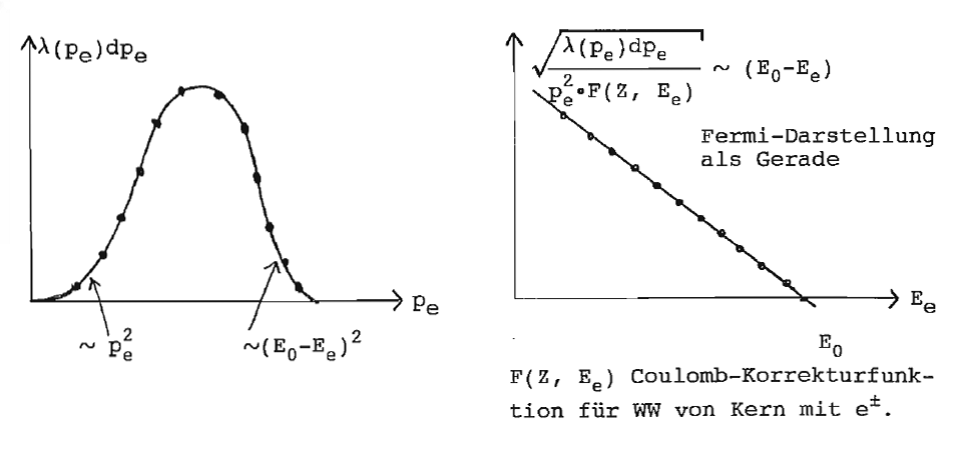
Durch Extrapolation bei der Fermi-Darstellung Bestimmung von . Damit auch die Möglichkeit zur Bestimmung einer möglichen Neutrinomasse, deren Existenz einen großen Einfluß auf Struktur und Entwicklung des Universums hat. Dabei wegen Fehlerabschätzung E0 möglichst klein wählen, z. B. Tritium-Zerfall mit [ zur Zeit ].
Integration über Impulsspektrum:
Die f-Werte sind tabelliert [2]. Sie enthalten die gesamte Energieabhängigkeit.
Grobe Abschätzung:
Bei genauerer Betrachtung muß man berücksichtigen, daß die Spins
der beiden Leptonen parallel (Gamow-Teller-Übergänge) oder antiparallel
(Fermi-Übergänge) stehen können. Für erlaubte Übergänge
() gelten somit die Auswahlregeln:
anschaulich:
Verbotene Übergänge:
Merkmal: größere Drehimpulsänderungen, größere ft1/ 2-Werte Beiträge für diese Übergänge aus: a) Reihenentwicklung der Leptonenwellenfunktionen
b) relativistische Wellenfunktionen der Nukleonen mit vN/c-Beiträge
Beispiele für erlaubte und verbotene Übergänge:
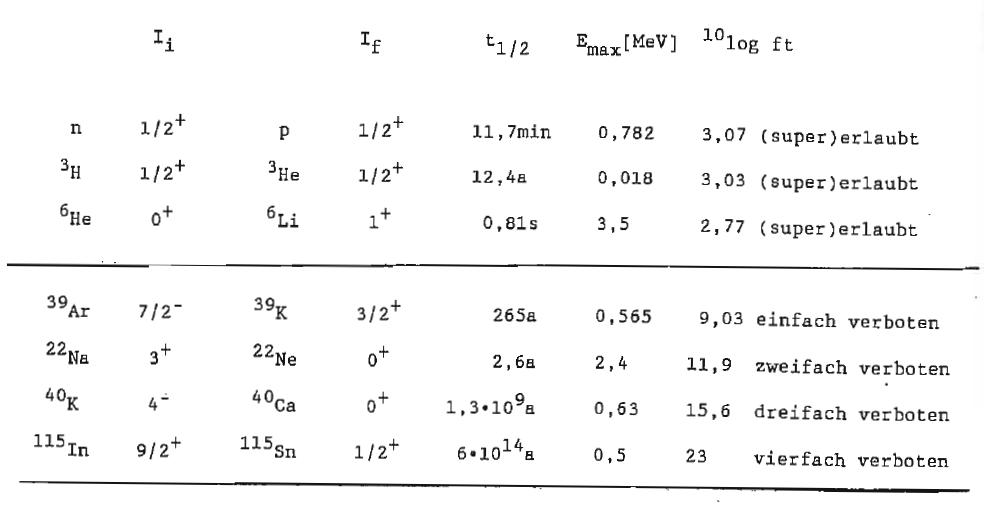
Einzelnachweise
Weitere Informationen
(gehört nicht zum Skript)
Prüfungsfragen
- ß Übergänge: Prinzipielle Reaktionsgleichung + Bethe-Weizsäcker
- Neutrinos: Was ist das wozu braucht man die (beim ß Zerfall)
- Besonderheit beim ß Zerfall? (siehe Kapitel Paritätsverletzung)
- Übergangsraten aus Fermis goldener Regel ("grobe" Herleitung)
- Fermi- und GT-Übergänge