Kernkräfte: Unterschied zwischen den Versionen
Die Seite wurde neu angelegt: „<noinclude>{{ScriptProf|Kapitel=8|Abschnitt=0|Prof=Prof. Dr. P. Zimmermann|Thema=Kern- und Strahlungsphysik|Schreiber=Moritz Schubotz}}</noinclude>“ |
|||
| (20 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
<noinclude>{{ScriptProf|Kapitel=8|Abschnitt=0|Prof=Prof. Dr. P. Zimmermann|Thema=Kern- und Strahlungsphysik|Schreiber=Moritz Schubotz}}</noinclude> | <noinclude>{{ScriptProf|Kapitel=8|Abschnitt=0|Prof=Prof. Dr. P. Zimmermann|Thema=Kern- und Strahlungsphysik|Schreiber=Moritz Schubotz}}</noinclude> | ||
Wegen <math>B/A \approx const \to</math> Kräfte immer nur zwischen zwei Nukleonen. Einfachste | |||
Modellsysteme: | |||
*a) das Deuteron und | |||
*b) n-p Streuung | |||
== Deuteron == | |||
Das Deuteron als einfachstes gebundenes Nukleonensystem mit folgenden Eigenschaften | |||
:1) Bindungsenergie <math>n + p \to d + 2,2 MeV</math> | |||
:2) {{FB|Kernspin}} <math>I = 1</math>, {{FB|magnetisches Kerndipolmoment}} <math>\mu_I = 0,857 ... \mu_K</math> (<math>\mu_I \approx \mu_p + \mu_n = 0,879 ... \mu_K \to I = \tfrac{1}{2} + \tfrac{1}{2} , {}^3S_1</math>-Zustand) elektrisches Quadrupolmoment <math>Q = +2,86 10^{-31} {\rm m^2} = 2,7{\rm mb}</math>, d.h. sehr klein | |||
:3) es existiert kein angeregter Zustand, außerdem gibt es '''kein''' Diproton oder Dineutron. | |||
Reduktion des {{FB|Zweikörperproblem}}s durch Relativkoordinate <math>r = r -r_n</math> und red. Masse <math>\mu = \frac{m_p m_n}{m_p+m_n}\approx \frac{1}{2}m_p</math> | |||
Schrödingergleichung <math>\left[ \frac{-\hbar^2}{2\mu} \nabla^2 + V \right] \Psi = E \Psi</math> | |||
Problem <math>E = -2,2 MeV</math> bekannt, V unbekannt. | |||
Annahme: <math>V = V(r)</math> Zentralpotential. | |||
Separationsansatz von Radial- und Winkelteil <math>\Psi_{nlm}=R_{nl}(r) Y_{lm}(\theta, \phi)</math> | |||
Radialteil <math>\left[ - \frac{\hbar^2}{2\mu} \frac{d^2}{dr^2}+V(r) + \frac{l(l+1) \hbar ^2}{2 \mu r^2}\right] \left( r R_{nl} \right) = E_{nl} (rR_{nl})</math> mit <math>\frac{l(l+1) \hbar ^2}{2 \mu r^2}</math> Zentrifugalpotential | |||
Zentrifugalpotential abstoßend --> Grundzustand 1 = 0 (wird durch I = 1 und <math>\mu_I \approx \mu_n+\mu_p</math> unterstützt). <math>(rR_{nl} ) = (rR_{l0} )= u</math> | |||
Erste (grobe) Annahme von V(r): Kastenpotential (<math>V_0,r_0</math> ) | |||
[[Datei:8.1.Kastenpotential.png|miniatur|Trennung der Radialgleichung in Innen(I)- und Außen (II)-Bereich]] | |||
'''Innen (I):''' <math>r \le r_0 \frac{d^2u}{dr^2}+\frac{2 \mu}{\hbar^2}(E-V_0) u =0</math> , <math>K = \sqrt{\frac{2\mu(E-V_0)}{\hbar^2}}</math> | |||
Lösung <math>u = A \sin Kr + C\cos Kr RB: u = A \sin Kr</math> RB: <math>u=0</math> für <math>r \to 0</math> wegen u/r endlich C = 0 | |||
---- | |||
'''Außen (II):''' <math>r \ge r_0 \frac{d^2u}{dr^2}+\frac{2 \mu}{\hbar^2}(E) u =0</math> , <math>k = \sqrt{\frac{2\mu E}{\hbar^2}}=[4,3 10^{-15}m]^{-1}</math> | |||
Lösung <math>u = B' e^{-kr} + D e^{kr} = B e^{-k(r-r_0)}</math> RB: u = A \sin Kr</math> RB: <math>u\to0</math> für <math>r \to \infty \to </math> D=0 | |||
Stetiger Anlschluß von u und <math>\frac{du}{dr}</math> bei <math>r = r_0</math>: | |||
:<math>\begin{align} | |||
A\sin Kr_0 &= B \\ | |||
K A \cos Kr_0 &= B (-k)\\ | |||
\to K \operatorname{ctg} K r_0 &= -k | |||
\end{align}</math> | |||
Damit werden die beiden Parameter (<math>V_0,r_0</math>) des Kastenpotentials miteinander | |||
verknüpft, z.B. mögliche Wertepaare | |||
:<math>\begin{align} | |||
r_0 &= 1,4 \times 10^{-15} m, &2 \times 10^{-15} m\\ | |||
V_0 &= 50 MeV, &30 MeV | |||
\end{align}</math> | |||
[[Datei:8.2.Kastenpotential.Vernbessert.png|miniatur]] | |||
Da für <math>\vec I =\vec \tfrac{1}{2} +\vec \tfrac{1}{2}</math> nur I = 1 existiert, sind die Kernkräfte '''spinabhängig''', | |||
wobei nur das Triplettpotential bindend ist. | |||
Erklärt auch die Nichtexistenz von <math>p^2</math> und <math>n^2</math> durch das Pauli-Prinzip. | |||
*Ansatz <math>V =V_1(r) + V_2 (r)(\vec s_1 \vec s_2 ) \quad (\vec s_1 \vec s_2 ) \Rightarrow \frac{1}{2}\left[S(S+1)-\frac{3}{4}-\frac{3}{4}\right]</math> | |||
*{{FB|Triplett}} <math>V_T = V_1 (r) +\frac{1}{4}V_2 (r), \quad S = 1</math> | |||
*{{FB|Singulett}} <math>V_S = V_1 (r) -\frac{3}{4}V_2 (r), \quad S = 0</math> | |||
Grobe Abschätzung für Singulett-Potential: | |||
Falls <math>V_s</math> gerade nicht mehr bindend <math>\to \sin Kr_0 \approx 1</math> senkrecht auf Potentialwand, so daß man keine abnehmende Exponentialfunktion im | |||
Außenraum anfügen kann. | |||
<math>Kr_0 \le \frac{\pi}{2}</math> bedeutet in Zahlenwerten <math>|V_0|r_0^2 \lesssim 100,\quad V_0 [MeV], r_0 [10^{-15} m]</math> | |||
Die Existenz des (sehr kleinen) Quadrupolmoments bedeutet einen sehr kleinen Beitrag einer '''nichtzentralen''' Kraft, | |||
die eine <math>^3D_1</math>-Zumischung ermöglicht. | |||
== n-p Streuung == | |||
Wirkungsquerschnitt <math>\sigma[m^2]</math> | |||
[[Datei:8.3.Wirkungsquerschnitt.png|zentriert|miniatur|hochkant=2|Wikungsquerschnitt für Protonen Neutronen Streuung]] | |||
<math>\sigma</math> als "Trefferfläche" , z.B. <math>\sigma(geom.) = \pi R^2 \approx 10^{-29}-10^{-28} m^2 (10^{-28}m^2 | |||
= 1b)</math>. Festkörpertarget <math>N \approx 10^{22}</math> Kerne/cm³, <math>\sigma \approx 10^{28}m^{-3}</math>, Targetlänge | |||
z.B. <math>1 = 10^{-2}m \to \sigma Nl \approx 10^{-3}-10^{- 2}</math> , d.h. "dünnes" Target mit <math>I =I_0 (l-\sigma Nl)</math>. | |||
Kinematik: <math>m_p \approx m_n</math>, "Billardproblem" | |||
[[Datei:8.4.Zweikoerperproblem.png|zentriert|miniatur|hochkant=2|Protonen Neutronen Streuung in verschiedenen Bezugssystemen]] | |||
<math>2 \to 1</math> Körperproblem: Stoß zweier Teilchen gleicher Masse im CM-System | |||
ist äquivalent dem Stoß eines Teilchens mit reduzierter Masse <math>\mu = m/2</math> und <math>E = E_{LAB}/2</math> an einem festen Streuzentrum bei | |||
<math>r=r_p - r_p \approx 0</math>. | |||
Quantenmechanische Formulierung des Streuproblems | |||
[[Datei:8.5.Streuproblem.Quantenemechanische.Formulierung.png|zentriert|miniatur|hochkant=2|Quantenmechanische Formulierung für Protonen Neutronen Streuung]] | |||
{{FB|differentieller Wirkungsquerschnitt}} <math>d\sigma/d\Omega</math> in Raumwinkel <math>d\Omega</math>: | |||
{{Gln| | |||
:<math>\frac{d\sigma}{dn}=\frac{\text{ Fluss der gestreuten Teilchen in Raumwinkel d}{\Omega}\text{(Detektor)}}{\text{Fluss der einlaufenden Teilchen pro Einheitsflaeche}}</math>|Differentieller Wirklungsquerschnitt}} | |||
;Fluß der einfallenden Teilchen: <math>|e^{ikz}|^2 v</math>, <math>|e^{ikz}|^2 </math> 1 Teilchen pro Raumeinheit | |||
;Fluß der gestreuten Teilchen in <math>d\Omega:|e^{ikr} f(\theta)|^2 r^2 v \to</math> | |||
:<math>\frac{d \sigma}{d\Omega} = |f(\theta)|^2</math> Quadrat der Streuamplitude <math>f(\theta)</math> | |||
Speziell für {{FB|isotrope Streuung}} <math>(f(\sigma) = const.)</math> ist dann der (Gesamt)-{{FB|Wirkungsquerschnitt}} | |||
:<math>\sigma = 4 \pi |f|^2</math> . | |||
===Berechnung des Wirkungsquerschnitts:=== | |||
Zunächst Entwicklung der einlaufenden ebenen Welle nach Kugelwellen. | |||
:<math>e^{ikz} = e^{ikr\cos\theta} =\sum_1 i^l (2l+1) j_l(kr)P_1(cos\theta)</math> | |||
:<math>j_l(kr)</math> sphärische Besselfunktionen | |||
Sinn: Bei niedrigen Energien (<math>E_n \le 10 \rm MeV</math>) kann wegen der kurzen | |||
Reichweite der Kernkräfte nur der <math>1 = O</math>-Anteil (S-Wellen) gestreut | |||
werden. Teilchen mit <math>1 \neq 0</math> kommen bei diesen Energien nicht nahe | |||
genug heran. | |||
Quantitativ: | |||
[[Datei:8.6.SWellenAnteil.png|miniatur|zentriert|hochkant=3]] | |||
Wegen <math>k=\sqrt{\frac{2 \mu E}{\hbar^2}}= 0,15\sqrt{\tfrac{1}{2}E_{LAB}[MeV]} 10^{15} m^{- l}</math> | |||
und <math>r_0= 10^{-15}</math>m ist für <math>E_{LAB}\le MeV</math> | |||
die Bedingung <math>kr_0 \le 1</math> erfüllt. | |||
Der S-Wellenanteil der einlaufenden ebenen Welle lautet mit <math>j_0(kr)</math>: | |||
:(S-Wellenanteil) <math>=\frac{\sin kr}{kr}\equiv \frac{e^{ikr}-e^{-ikr}}{2ikr}</math>, <math>e^{ikr}</math> auslaufende Kugelwelle, <math>e^{-ikr}</math> einlaufende Kugelwelle | |||
Nach dem "Durchlaufen" des Zentralpotentials <math>V = V(r)</math> bleiben der | |||
S-Wellencharakter, der Wellenvektor <math>k</math> und die Teilchenzahl erhalten. | |||
Deshalb kann es nur eine '''Phasenänderung''' in der '''auslaufenden Kugelwelle''' geben. | |||
S-Wellenanteil nach Durchlaufen des Streupotentials: | |||
:<math>\frac{e^{i (kr+2\delta_0)}- e^{ikr}}{2ikr} \equiv e^{i\delta_0} \frac{\sin(kr+\delta_0)}{kr}</math> | |||
Die Differenz des S-Wellenanteils vor und nach der Streuung charakterisiert | |||
die qestreuten Teilchen, also die gestreute auslaufende Kugelwelle <math>\frac{e^{ikr}}{r} f(\theta)</math>: | |||
:<math>\frac{e^{i(kr+2\delta_{0}}-e^{ikr}}{2ikr}\equiv\frac{e^{i(kr+\delta_{0}})}{r}\frac{\sin\delta_{0}}{k}</math> | |||
Damit gilt für den diff. Wirkungsquerschnitt in Abhängigkeit von der Streuphase <math>\delta_0</math> | |||
:<math>\frac{d \sigma}{d \Omega} = | f(\theta)|^2= \frac {\sin^2\delta_0}{k^2}</math> | |||
Berechnung der Streuphase mit einem Kastenpotential (<math>V_0,r_0</math>) über | |||
die Schrödingergleichung analog zum Deuteronproblem, jedoch <math>E > O</math>. | |||
{| class="wikitable center" | |||
|- | |||
!Innenbereich I !! Außenbereich II | |||
|- | |||
| <math>\left[\frac{h^2}{2\mu}\frac{d^2}{dr^2}+V_0\right] u = E u</math> || <math>\left[\frac{h^2}{2\mu}\frac{d^2}{dr^2}+0\right] u = E u</math> | |||
|- | |||
| <math>u=A_1 \sin Kr</math> || <math>u=A_1 \sin( kr+\delta_0)</math> | |||
|- | |||
| <math>K=\sqrt\frac{2\mu(E-V_0)}{\hbar^2}</math> || <math>k=\sqrt\frac{2\mu(E)}{\hbar^2}</math> (siehe <math>e^{i\delta_0}\frac{\sin(kr+\delta_0)}{kr}</math> und <math>\Psi \sim \frac{u}{r}</math> | |||
|} | |||
Stetige Anpassung für <math>u</math> und <math>du/dr</math> bei <math>r = r_0</math> ergibt | |||
:<math>\begin{align} | |||
A_1 \sin Kr_0 &= A_2 \sin (k r_0 +\delta_0) &=A_2 k (r_0-a)\\ | |||
K A_1 \cos Kr_0 &= k A_2 \cos (k r_0 +\delta_0) &=A_2 k\\[0.5em] | |||
K \cot Kr_0 &= \cot (k r_0 +\delta_0) &= \underbrace{(r_0-a)^{-1}}_{k \ll K}\\ | |||
\end{align}</math> | |||
Im niederenergetischen Bereich mit <math>k \ll K</math> kann man die Sinusfunktion | |||
im Außenbereich durch eine Gerade ersetzen | |||
:<math>u \simeq A_2 (kr+\delta_0) = A_2 k(r-a)</math> mit <math>\delta_0 = -ka</math>. | |||
Die sogenannte {{FB|Streulänge}} <math>a</math> ist der Schnittpunkt dieser Geraden mit der r-Achse. Je nachdem (<math>V_0,r_0</math>) für <math>E \approx 0</math> bindend oder nichtbindend ist, ist a positiv oder negativ. Sehr große Werte für die | |||
Streulänge erhält man, wenn das Potential gerade noch (<math>V_T</math>) oder | |||
gerade nicht mehr bindend (<math>V_S</math>) ist. | |||
[[Datei:8.7.Wirkungsquerschnitt.Kasten.QM.png|miniatur|zentriert|hochkant=2|Wellefunktion fürStreulänge für Singulett, Triplett etc]] | |||
Wirkungsquerschnitt <math>\sigma = 4\pi|f(\theta)|^2 = 4\pi \frac{\sin^2 \delta_0 }{k^2} = 4 \pi a^2</math> | |||
unabhängig von E für den Bereich <math>k \le K</math> mit <math>\delta_0 = -ka</math> und <math>a = | |||
r_ 0-\frac{1}{K} tg Kr_0 </math>. In der Streu1änge a sind wieder die beiden Parameter | |||
des Kastenpotentials (<math>V_0, r_0</math>) miteinander verknüpft. | |||
Experimentell: | |||
[[Datei:8.8.Wirkungsquerschnitt.Experimentell.png|miniatur|zentriert|hochkant=2|Totaler Wirkungsquerschnitt als Funktion der Neutronenenergie]] | |||
Grobe Abschätzung aus {{FB|Deuteronproblem}} ergibt für das {{FB|Triplettpotential}} | |||
:<math>a_T = 5,7\times 10^{-15}m</math> und damit <math>\sigma_T \approx 4,5\times 10^{-28}m^2</math>. | |||
Damit erhält man aus <math>\sigma \approx 20\times 10^{-28}m^2</math> für <math>\sigma_S \approx 68 \times 10^{-28}m^ 2</math> und | |||
:<math>|a_S| = 23\times 10^{- 28}m^2</math>. Das negative Vorzeichen <math>a_S < 0</math> folgt aus Messungen der kohärenten | |||
Streuung am Para-Wasserstoff-Molekül. | |||
Während der Bereich bis ca. | |||
:<math>10^4</math> eV vom '''Singulett-Potential''' beherrscht wird, tritt für den Bereich | |||
:<math>10^4 - 10^7</math> eV immer mehr das '''Triplett-Potential''' in den Vordergrund. Ab | |||
:<math>10^7</math> eV müssen verstärkt '''höhere Bahndrehimpulsanteile''' berücksichtigt werden. | |||
Bei einer feldtheoretischen Behandlung in Analogie zur Quantenelektrodynamik | |||
versucht man die Kernkräfte durch {{FB|Mesonen-Austauschprozesse}} zu beschreiben. Dabei wird der "langreichweitige" | |||
Teil durch {{FB|Ein-Pion-Austauschprozess}}e (Yukawa-Ansatz 1935) und der Bereich mittlerer Reichweite durch {{FB|Zwei-Pion-Austauschprozess}}e beschrieben. | |||
Der "kurzreichweitige" Teil mit einem stark abstoßenden Anteil (''hard core'') muß durch den Austausch mehrerer Mesonen behandelt | |||
werden. Dabei spielen nicht nur die <math>\omega</math>-Mesonen, sondern schwere | |||
Mesonen (z.B. das <math>\omega</math>-Meson mit <math>mc^2 = 783 MeV</math>) wegen ihrer | |||
'''kleinen Compton-Wellenlänge''' eine besondere Rolle. Da Nukleonen und | |||
Mesonen ihrerseits aus {{FB|Quarks}} zusammengesetzt sind, die von {{FB|Gluonen}} zusammengehalten werden, muß eine genauere Feldtheorie der | |||
Kernkräfte auf diesen Teilchen aufbauen. | |||
==Ergänzende Informationen== | |||
(gehört nicht zum Skript) | |||
===Prüfungsfragen=== | |||
*Was ist das besondere der starken und schwachen WW? -> sehr kurze Reichweite | |||
* Analogie QCD -> \pi , QED -> \gamma (Quarks als Grundbaustein der Hadronen mit Gluonen als Austauschteilehen und Pionen als Austauschteilehen der Hadronen im Atomkern (Yukawa Potential), nur erwähnt, Quarks und Leptonen (speziell Elektronen) sind Punkteilchen) | |||
Aktuelle Version vom 28. August 2011, 15:32 Uhr

|
Der Artikel Kernkräfte basiert auf der Vorlesungsmitschrift von Moritz Schubotz des 8.Kapitels (Abschnitt 0) der Kern- und Strahlungsphysikvorlesung von Prof. Dr. P. Zimmermann. |
Die Abfrage enthält eine leere Bedingung.
Wegen Kräfte immer nur zwischen zwei Nukleonen. Einfachste
Modellsysteme:
- a) das Deuteron und
- b) n-p Streuung
Deuteron
Das Deuteron als einfachstes gebundenes Nukleonensystem mit folgenden Eigenschaften
- 1) Bindungsenergie
- 2) Kernspin , magnetisches Kerndipolmoment (-Zustand) elektrisches Quadrupolmoment , d.h. sehr klein
- 3) es existiert kein angeregter Zustand, außerdem gibt es kein Diproton oder Dineutron.
Reduktion des Zweikörperproblems durch Relativkoordinate und red. Masse
Schrödingergleichung
Problem bekannt, V unbekannt.
Annahme: Zentralpotential. Separationsansatz von Radial- und Winkelteil
Radialteil mit Zentrifugalpotential
Zentrifugalpotential abstoßend --> Grundzustand 1 = 0 (wird durch I = 1 und unterstützt).
Erste (grobe) Annahme von V(r): Kastenpotential ( )
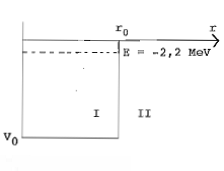
Innen (I): ,
Lösung RB: für wegen u/r endlich C = 0
Außen (II): ,
Lösung RB: u = A \sin Kr</math> RB: für D=0
Stetiger Anlschluß von u und bei :
Damit werden die beiden Parameter () des Kastenpotentials miteinander verknüpft, z.B. mögliche Wertepaare
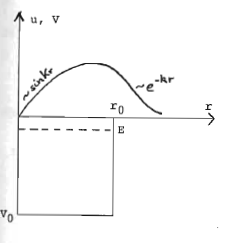
Da für nur I = 1 existiert, sind die Kernkräfte spinabhängig, wobei nur das Triplettpotential bindend ist. Erklärt auch die Nichtexistenz von und durch das Pauli-Prinzip.
Grobe Abschätzung für Singulett-Potential:
Falls gerade nicht mehr bindend senkrecht auf Potentialwand, so daß man keine abnehmende Exponentialfunktion im Außenraum anfügen kann.
bedeutet in Zahlenwerten
Die Existenz des (sehr kleinen) Quadrupolmoments bedeutet einen sehr kleinen Beitrag einer nichtzentralen Kraft,
die eine -Zumischung ermöglicht.
n-p Streuung
Wirkungsquerschnitt
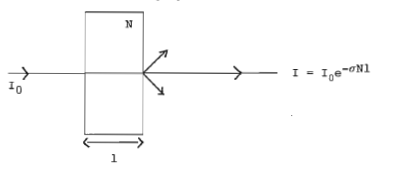
als "Trefferfläche" , z.B. . Festkörpertarget Kerne/cm³, , Targetlänge z.B. , d.h. "dünnes" Target mit .
Kinematik: , "Billardproblem"
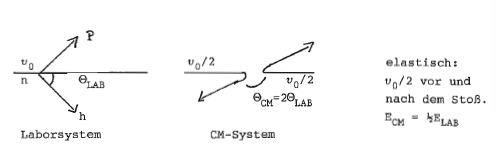
Körperproblem: Stoß zweier Teilchen gleicher Masse im CM-System ist äquivalent dem Stoß eines Teilchens mit reduzierter Masse und an einem festen Streuzentrum bei .
Quantenmechanische Formulierung des Streuproblems
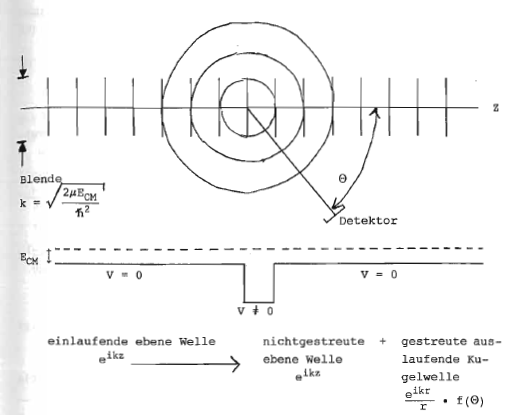
differentieller Wirkungsquerschnitt in Raumwinkel :
|
|
- Fluß der einfallenden Teilchen
- , 1 Teilchen pro Raumeinheit
- Fluß der gestreuten Teilchen in
- Quadrat der Streuamplitude
Speziell für isotrope Streuung ist dann der (Gesamt)-Wirkungsquerschnitt
- .
Berechnung des Wirkungsquerschnitts:
Zunächst Entwicklung der einlaufenden ebenen Welle nach Kugelwellen.
- sphärische Besselfunktionen
Sinn: Bei niedrigen Energien () kann wegen der kurzen Reichweite der Kernkräfte nur der -Anteil (S-Wellen) gestreut werden. Teilchen mit kommen bei diesen Energien nicht nahe genug heran.
Quantitativ:

Wegen und m ist für die Bedingung erfüllt.
Der S-Wellenanteil der einlaufenden ebenen Welle lautet mit :
- (S-Wellenanteil) , auslaufende Kugelwelle, einlaufende Kugelwelle
Nach dem "Durchlaufen" des Zentralpotentials bleiben der S-Wellencharakter, der Wellenvektor und die Teilchenzahl erhalten. Deshalb kann es nur eine Phasenänderung in der auslaufenden Kugelwelle geben.
S-Wellenanteil nach Durchlaufen des Streupotentials:
Die Differenz des S-Wellenanteils vor und nach der Streuung charakterisiert die qestreuten Teilchen, also die gestreute auslaufende Kugelwelle :
Damit gilt für den diff. Wirkungsquerschnitt in Abhängigkeit von der Streuphase
Berechnung der Streuphase mit einem Kastenpotential () über die Schrödingergleichung analog zum Deuteronproblem, jedoch .
| Innenbereich I | Außenbereich II |
|---|---|
| (siehe und |
Stetige Anpassung für und bei ergibt
Im niederenergetischen Bereich mit kann man die Sinusfunktion im Außenbereich durch eine Gerade ersetzen
- mit .
Die sogenannte Streulänge ist der Schnittpunkt dieser Geraden mit der r-Achse. Je nachdem () für bindend oder nichtbindend ist, ist a positiv oder negativ. Sehr große Werte für die Streulänge erhält man, wenn das Potential gerade noch () oder gerade nicht mehr bindend () ist.
Wirkungsquerschnitt unabhängig von E für den Bereich mit und . In der Streu1änge a sind wieder die beiden Parameter des Kastenpotentials () miteinander verknüpft.
Experimentell:
Grobe Abschätzung aus Deuteronproblem ergibt für das Triplettpotential
- und damit .
Damit erhält man aus für und
- . Das negative Vorzeichen folgt aus Messungen der kohärenten
Streuung am Para-Wasserstoff-Molekül.
Während der Bereich bis ca.
- eV vom Singulett-Potential beherrscht wird, tritt für den Bereich
- eV immer mehr das Triplett-Potential in den Vordergrund. Ab
- eV müssen verstärkt höhere Bahndrehimpulsanteile berücksichtigt werden.
Bei einer feldtheoretischen Behandlung in Analogie zur Quantenelektrodynamik
versucht man die Kernkräfte durch Mesonen-Austauschprozesse zu beschreiben. Dabei wird der "langreichweitige"
Teil durch Ein-Pion-Austauschprozesse (Yukawa-Ansatz 1935) und der Bereich mittlerer Reichweite durch Zwei-Pion-Austauschprozesse beschrieben.
Der "kurzreichweitige" Teil mit einem stark abstoßenden Anteil (hard core) muß durch den Austausch mehrerer Mesonen behandelt werden. Dabei spielen nicht nur die -Mesonen, sondern schwere Mesonen (z.B. das -Meson mit ) wegen ihrer kleinen Compton-Wellenlänge eine besondere Rolle. Da Nukleonen und Mesonen ihrerseits aus Quarks zusammengesetzt sind, die von Gluonen zusammengehalten werden, muß eine genauere Feldtheorie der Kernkräfte auf diesen Teilchen aufbauen.
Ergänzende Informationen
(gehört nicht zum Skript)
Prüfungsfragen
- Was ist das besondere der starken und schwachen WW? -> sehr kurze Reichweite
- Analogie QCD -> \pi , QED -> \gamma (Quarks als Grundbaustein der Hadronen mit Gluonen als Austauschteilehen und Pionen als Austauschteilehen der Hadronen im Atomkern (Yukawa Potential), nur erwähnt, Quarks und Leptonen (speziell Elektronen) sind Punkteilchen)








![{\displaystyle \left[{\frac {-\hbar ^{2}}{2\mu }}\nabla ^{2}+V\right]\Psi =E\Psi }](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f328f1867f0fb9c7a952db65cc788d076075c3f)



![{\displaystyle \left[-{\frac {\hbar ^{2}}{2\mu }}{\frac {d^{2}}{dr^{2}}}+V(r)+{\frac {l(l+1)\hbar ^{2}}{2\mu r^{2}}}\right]\left(rR_{nl}\right)=E_{nl}(rR_{nl})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cfa1d4eefe88da1fe39f4897285c6ce42ecd6ef9)










![{\displaystyle k={\sqrt {\frac {2\mu E}{\hbar ^{2}}}}=[4,310^{-15}m]^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f9402eadc8782e311df61acabd9733d4fdc9d85)










![{\displaystyle V=V_{1}(r)+V_{2}(r)({\vec {s}}_{1}{\vec {s}}_{2})\quad ({\vec {s}}_{1}{\vec {s}}_{2})\Rightarrow {\frac {1}{2}}\left[S(S+1)-{\frac {3}{4}}-{\frac {3}{4}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99c3ed89a186bc9f8f801d4cbde3b40469a98037)





![{\displaystyle |V_{0}|r_{0}^{2}\lesssim 100,\quad V_{0}[MeV],r_{0}[10^{-15}m]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9008987aa13d8805bf995464a0a1e3e2f2a4abb9)

![{\displaystyle \sigma [m^{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c9f1871c3c946dd1ce20b8e1dd2094d42849e00)


























![{\displaystyle k={\sqrt {\frac {2\mu E}{\hbar ^{2}}}}=0,15{\sqrt {{\tfrac {1}{2}}E_{LAB}[MeV]}}10^{15}m^{-l}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2db58753368ff3f54638ed05c9e16502b288ee82)














![{\displaystyle \left[{\frac {h^{2}}{2\mu }}{\frac {d^{2}}{dr^{2}}}+V_{0}\right]u=Eu}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c66a622c7210bacba2856f9ff0db9044c862dd25)
![{\displaystyle \left[{\frac {h^{2}}{2\mu }}{\frac {d^{2}}{dr^{2}}}+0\right]u=Eu}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b2ade8451c078abb8cfd2b664d01a135ff31cd9)







![{\displaystyle {\begin{aligned}A_{1}\sin Kr_{0}&=A_{2}\sin(kr_{0}+\delta _{0})&=A_{2}k(r_{0}-a)\\KA_{1}\cos Kr_{0}&=kA_{2}\cos(kr_{0}+\delta _{0})&=A_{2}k\\[0.5em]K\cot Kr_{0}&=\cot(kr_{0}+\delta _{0})&=\underbrace {(r_{0}-a)^{-1}} _{k\ll K}\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8035e105d6d9d6c744162ea6d9680491e86dea59)




















